Question

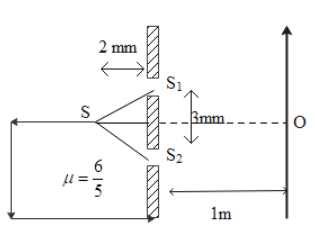
Find the order of the fringe formed at O.

Answer 1

Hint: First calculate the path difference at O. The path difference here is the difference between the $S{{S}_{2}}\And S{{S}_{1}}$since, the distances ${{S}_{1}}O\And {{S}_{2}}O$ are equal. Then calculate the thickness, t. Also path difference is the product of its wavelength and order of the fringe. Thus by rearranging the equation and substituting the values of wavelength and path difference we will get the order of the fringe.

Complete answer:
The path difference is denoted by the letter $\vartriangle x$ .
Hence,
$\begin{align}
  & \vartriangle x=\left( S{{S}_{2}}+{{S}_{2}}O \right)-\left( S{{S}_{1}}+{{S}_{1}}O \right) \\
 & \Rightarrow \vartriangle x=S{{S}_{2}}-S{{S}_{1}} \\
\end{align}$
That is, the distances ${{S}_{1}}O\And {{S}_{2}}O$ are equal.
Then thickness t is,
$t=\sqrt{{{2}^{2}}+{{1.5}^{2}}}=2.5mm$
Then,
$\begin{align}
  & \vartriangle x=\mu t-t \\
 & \Rightarrow \vartriangle x=\left( \dfrac{6}{5}\times 2.5 \right)-2.5 \\
 & \Rightarrow \vartriangle x=0.5mm \\
\end{align}$
The path length difference must be an integral multiple of the wavelength.
So, $\vartriangle x=n\lambda $
$\Rightarrow n=\dfrac{\vartriangle x}{\lambda }$
Substituting the value we get,
$\begin{align}
  & n=\dfrac{0.5\times {{10}^{-3}}}{500\times {{10}^{-9}}} \\
 & \therefore n=1000 \\
\end{align}$

Additional information:
$\dfrac{(2n-1){{\lambda }_{1}}D}{2d}=\dfrac{(2m-1){{\lambda }_{2}}D}{2d}$
where, d is the distance between the slits.
D, the distance between the slit and screen.
${{\lambda }_{1}}\And {{\lambda }_{2}}$ are the wavelengths of light used.
m and n are the order of interference.
 To obtain constructive interference for a double slit, the path length difference must be an integral multiple of the wavelength.
$d\sin \theta =m\lambda $
 For m= 0,1,-1,2,-2,…… (Constructive interference)
$d\sin \theta =\left( m+\dfrac{1}{2} \right)\lambda $
For m=0,1,-1,2,-2,……….(Destructive interference)
Here, $\lambda $ is the wavelength of light, d is the distance between the slits and m is the order of interference.

Note:
The value of m and n should not be a decimal or a fractional number. The path difference here is the difference between the $S{{S}_{2}}\ and S{{S}_{1}}$ since, the distances ${{S}_{1}}O\And {{S}_{2}}O$ are equal. Also path difference is the product of its wavelength and order of the fringe. To obtain constructive interference for a double slit, the path length difference must be an integral multiple of the wavelength.