Question

Find the point on x - axis which is equidistant from (2, -5) and (-2, 9).

Answer 1

Hint:As the given point is on the x-axis, we know that the point will be in the form of (x, 0), so we will find the distance between (x, 0) and (2, -5) and compare that with the distance between (x, 0) and (-2, 9) to get the value of x and thus the required answer.

Complete step by step answer:

In the question, we have been given a pair of points, that is (2, -5) and (-2, 9) and are asked to find a point such that it is equidistant to both the given points. It is given that the point should be on the x -axis, which means that its coordinate will be 0. And we know that this point will be in the form (x, 0), where x is a variable value. So, we will now find the distance between the given points and this, that is we will find the distance between (x, 0) and (2, -5) and then equate it with the distance between (x, 0) and (-2, 9) by using the distance formula, which is given by, $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$, if the points are $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$. So, we will get the distance between (x, 0) and (2, -5) as,
$\begin{align}
  & \sqrt{{{\left( x-2 \right)}^{2}}+{{\left( 0-\left( -5 \right) \right)}^{2}}} \\
 & \Rightarrow \sqrt{{{\left( x-2 \right)}^{2}}+25} \\
\end{align}$
And we can find the distance between (x, 0) and (-2, 9) as follows,
$\begin{align}
  & \sqrt{{{\left( x-\left( -2 \right) \right)}^{2}}+{{\left( 0-9 \right)}^{2}}} \\
 & \Rightarrow \sqrt{{{\left( x+2 \right)}^{2}}+81} \\
\end{align}$
We will now equate the distances, so we will get,
$\sqrt{{{\left( x-2 \right)}^{2}}+25}=\sqrt{{{\left( x+2 \right)}^{2}}+81}$
On squaring both the sides, we will get,
${{\left( x-2 \right)}^{2}}+25={{\left( x+2 \right)}^{2}}+81$
We will now subtract ${{\left( x-2 \right)}^{2}}+25$ from both the sides, so we get,
$\begin{align}
  & {{\left( x-2 \right)}^{2}}+25-\left( {{\left( x-2 \right)}^{2}}+25 \right)={{\left( x+2 \right)}^{2}}+81-\left( {{\left( x-2 \right)}^{2}}+25 \right) \\
 & \Rightarrow {{\left( x+2 \right)}^{2}}-{{\left( x-2 \right)}^{2}}+46=0 \\
\end{align}$
We will now use the identity, ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$, we will take $a=\left( x+2 \right),b=\left( x-2 \right)$. So, we will get,
$\begin{align}
  & \left( \left( x+2 \right)+\left( x-2 \right) \right)\left( \left( x+2 \right)-\left( x-2 \right) \right)+46=0 \\
 & \Rightarrow 2x\times 4+46=0 \\
 & \Rightarrow 8x+46=0 \\
 & \Rightarrow 8x=-46 \\
 & \Rightarrow x=\dfrac{-46}{8} \\
\end{align}$
Hence, we get the value of x as $\dfrac{-46}{8}$. Thus, the point on x - axis that is equidistant from both the points is $\left( \dfrac{-46}{8},0 \right)$ .

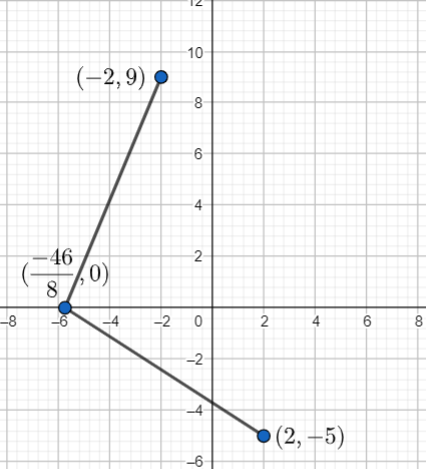
Note:
The students can recheck whether their solution is correct or not by finding the distance between the points and comparing whether they are equal or not. They should be careful while applying the distance formula and not mistake by writing the negative sign in place of the positive sign as, $\sqrt{{{\left( {{x}_{2}}+{{x}_{1}} \right)}^{2}}-{{\left( {{y}_{2}}+{{y}_{1}} \right)}^{2}}}$.