
Find the position vector of the a point lying on the line joining the points whose position vectors are
Answer
481.2k+ views
Hint: We recall the definition of position vectors. We use the fact that the position vector of any point P that lies on the line joining two points A,B whose positions vector are known as
Complete step by step answer:
We can represent any point in the space
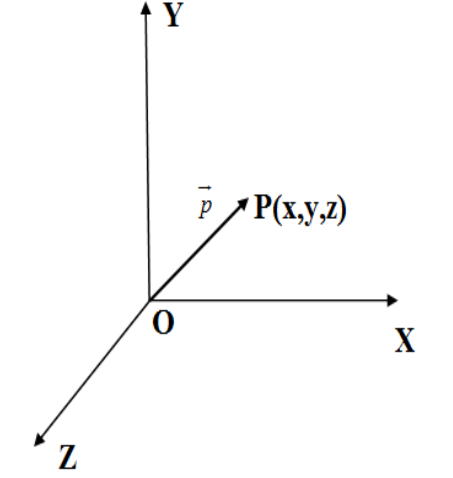
If there are
We are given in the question the position vectors of two points as
We compare the respective components and we get;
Let P be any point on the line segment joining A and B.The position vector of P is;
Note: We also know that
Complete step by step answer:
We can represent any point in the space
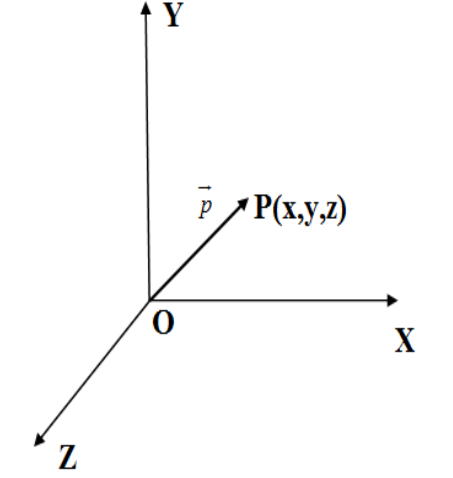
If there are
We are given in the question the position vectors of two points as
We compare the respective components and we get;
Let P be any point on the line segment joining A and B.The position vector of P is;
Note: We also know that
Recently Updated Pages
Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the difference between resemblance and sem class 12 social science CBSE




