Question

Find the principal value of $\cos e{{c}^{-1}}\left( 2 \right)$.

Answer 1

Hint: We will be using the concept of inverse trigonometric functions to solve the problem. We will first write 2 as $\cos ec\theta $ then we will use the fact that $\cos e{{c}^{-1}}\left( \cos ecx \right)=x$ for $x\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]-\left\{ 0 \right\}$.

Complete step by step answer:
Now, we have to find the value of $\cos e{{c}^{-1}}\left( 2 \right)$.
Now, we will first represent 2 in terms of cosecant of an angle. So, we know that the value of $\cos ec\left(\dfrac{\pi }{6} \right)$ is 2.
$2=\cos ec\left( \dfrac{\pi }{6} \right).........\left( 1 \right)$
We have taken $2=\cos ec\left(\dfrac{\pi }{6}\right)$ as in the view of the principal value convention x is confined to$x\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]-\left\{ 0 \right\}$.
Now, we know that the graph of $\cos e{{c}^{-1}}\left( \cos ecx \right)$ is,

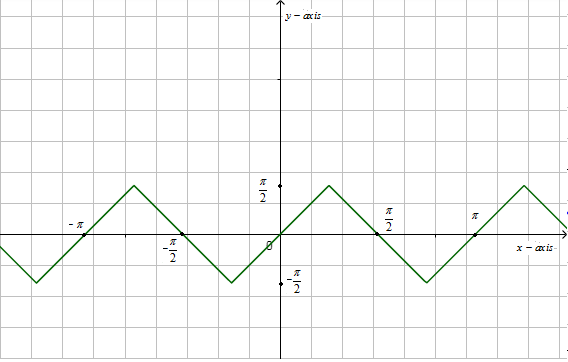
Now, we have to find the value of$\cos e{{c}^{-1}}\left( 2 \right)$.
We will use the equation (1) to substitute the value of 2. So, we have,
$\cos e{{c}^{-1}}\left( \cos ec\left( \dfrac{\pi }{6} \right) \right)$
Also, we know that $\cos e{{c}^{-1}}\left( \cos ecx \right)=x$. So, we have,
$\cos e{{c}^{-1}}\left( \cos ec\left( \dfrac{\pi }{6} \right) \right)=\dfrac{\pi }{6}$

So, the correct answer is “$\dfrac{\pi }{6}$”.

Note: To solve these type of question it is important to note that we have used a fact that $\cos e{{c}^{-1}}\left( \cos ecx \right)=x$ only for $x\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]-\left\{ 0 \right\}$. For another value of x the graph of $\cos e{{c}^{-1}}\left( \cos ecx \right)$ must be used to find the value.