Question

Find the principal value of \[{\tan ^{ - 1}}\left( {\cos \left( {\dfrac{\pi }{2}} \right)} \right)\].

Answer 1

Hint: The range of \[{\tan ^{ - 1}}\theta \] is between \[\left. {\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right.} \right)\]. From the trigonometric table find the value of \[\cos \dfrac{\pi }{2}\] . Now substitute this back into our given expression and simplify it to get the principal value.

Complete step-by-step answer:
A principal value of a function is the value selected at a point in the domain of a multiple-valued function, chosen so that the function has a single value at the point. The principal value of \[{\tan ^{ - 1}}\theta \]
The principal value of \[{\tan ^{ - 1}}\theta \] branches to,
\[{\tan ^{ - 1}}\theta \in \left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\].
Hence the principal value of the given function will be between the range\[\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\] .
Now we have been given the function, \[{\tan ^{ - 1}}\left( {\cos \left( {\dfrac{\pi }{2}} \right)} \right)\]. Let us put this function as equal to \[\theta \].
Thus we get,
\[{\tan ^{ - 1}}\left( {\cos \left( {\dfrac{\pi }{2}} \right)} \right) = \theta \]
\[\tan \theta = \cos \dfrac{\pi }{2}\].
Let us first find the value of \[\cos \dfrac{\pi }{2}\] from the above expression. By using the trigonometric table we can find the value of \[\cos \dfrac{\pi }{2}\] . Let us draw the trigonometric table to make the identification of the function easier.

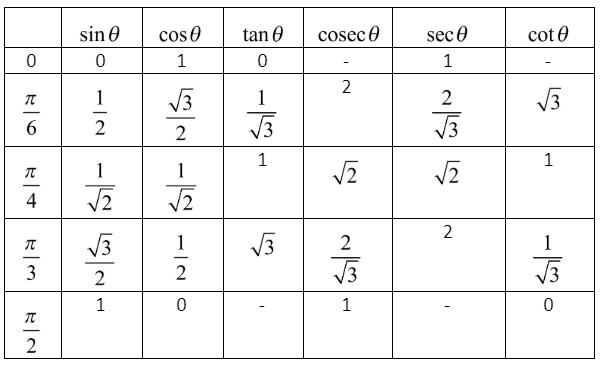
From the trigonometric table we can find that the value of \[\cos \dfrac{\pi }{2} = 0\]. Now substitute back the value of \[\cos \dfrac{\pi }{2}\] in the expression. Hence we get it as,
\[\tan \theta = \cos \dfrac{\pi }{2} = 0\] , thus we can write it as
\[
  \tan \theta = 0 \ \\
  \theta = {\tan ^{ - 1}}0 = 0 \ \\
  \theta = 0 \ \\
 \]
Thus we got the principal value here as zero.
\[\therefore {\tan ^{ - 1}}\left( {\cos \left( {\dfrac{\pi }{2}} \right)} \right) = 0\]

Note: To solve a question like these you should be familiar with the domain and range of the sine functions as well as the domain and range of the inverse sine functions. For us the range of inverse tangent function is \[\left( { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right)\] and the domain of inverse function of tangent is \[\left( { - \infty ,\infty } \right)\]. Students should remember the important trigonometric ratios and standard angles to solve these types of questions.