
Find the slant height of a frustum cone whose top radius is 12 m and bottom radius is 10 m. The height of the cone is 13 m.
A. 13.15 m
B. 12.15 m
C. 10.15 m
D. 14.25 m
Answer
570.6k+ views
Hint: First draw the diagram on the base of data provided in the question. After that find the difference between the top radius and the bottom radius. Then, use the Pythagoras theorem to find the slant height of the frustum by using the height and the difference of the radius of the frustum and simplify.
Complete step-by-step solution:
The diagram on basis of data provided in the question is,
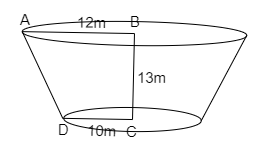
Draw a perpendicular from D on AB which meets at E.
Let the height of the frustum be AD.
As, DE is the distance from the top of the frustum to the bottom, which is the height of the frustum. So,
$ \Rightarrow DE = 13$m……………...….. (1)
Now find the length of AE.
As DE is perpendicular from D on AB. Then the length of BE is equal to the length of DC. So,
$ \Rightarrow BE = 10$m
Now, the length of AE is the difference between the length of AB and BE. So,
$ \Rightarrow AE = AB - BE$
Substitute the values,
$ \Rightarrow AE = 12 - 10$
Subtract the terms on the right side,
$ \Rightarrow AE = 2$m…………..….. (2)
Now, in $\Delta ADE$, apply Pythagoras Theorem,
$A{D^2} = D{E^2} + A{E^2}$
Substitute the values of DE and AE from equation (1) and (2),
$ \Rightarrow A{D^2} = {13^2} + {2^2}$
Square the terms on the right side,
$ \Rightarrow A{D^2} = 169 + 4$
Add the terms,
$ \Rightarrow A{D^2} = 173$
Take the square root on both sides,
$ \Rightarrow AD = \sqrt {173} $
Simplify the terms,
$\therefore AD = 13.15$m
Hence, the height of the frustum is 13.15 m.
Option A is the correct option.
Note: The students might make mistakes by not finding the difference of radius and then applying Pythagoras Theorem. It may lead to a lengthy calculation or even a wrong answer.
The slant height of a frustum of a right circular cone is the line segment joining the extreme point of two parallel radii, drawn in the same direction, of the two circular bases.
Complete step-by-step solution:
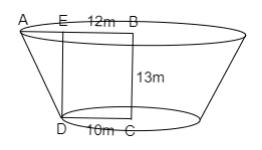
The diagram on basis of data provided in the question is,

Draw a perpendicular from D on AB which meets at E.

Let the height of the frustum be AD.
As, DE is the distance from the top of the frustum to the bottom, which is the height of the frustum. So,
$ \Rightarrow DE = 13$m……………...….. (1)
Now find the length of AE.
As DE is perpendicular from D on AB. Then the length of BE is equal to the length of DC. So,
$ \Rightarrow BE = 10$m
Now, the length of AE is the difference between the length of AB and BE. So,
$ \Rightarrow AE = AB - BE$
Substitute the values,
$ \Rightarrow AE = 12 - 10$
Subtract the terms on the right side,
$ \Rightarrow AE = 2$m…………..….. (2)
Now, in $\Delta ADE$, apply Pythagoras Theorem,
$A{D^2} = D{E^2} + A{E^2}$
Substitute the values of DE and AE from equation (1) and (2),
$ \Rightarrow A{D^2} = {13^2} + {2^2}$
Square the terms on the right side,
$ \Rightarrow A{D^2} = 169 + 4$
Add the terms,
$ \Rightarrow A{D^2} = 173$
Take the square root on both sides,
$ \Rightarrow AD = \sqrt {173} $
Simplify the terms,
$\therefore AD = 13.15$m
Hence, the height of the frustum is 13.15 m.
Option A is the correct option.
Note: The students might make mistakes by not finding the difference of radius and then applying Pythagoras Theorem. It may lead to a lengthy calculation or even a wrong answer.
The slant height of a frustum of a right circular cone is the line segment joining the extreme point of two parallel radii, drawn in the same direction, of the two circular bases.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




