
Find the square meters, the area of rectangle of length \[ = {\rm{12m}}\] and breadth \[ = {\rm{125cm}}\].
Answer
583.5k+ views
Hint: Find a formula for area of rectangle. Now substitute the values of variables you need to solve the equation. By this you will get the value of the area of the rectangle. This area is the required result in the question.
Complete step-by-step answer:
Rectangle: In Euclidean plane geometry, a rectangle is a quadrilateral with 4 right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal. It can also be defined as a parallelogram containing a right angle. It is a two-dimensional shape.
Besides the above definition we can also define the rectangle as a combination of strips of breadth db upto b each of length l.
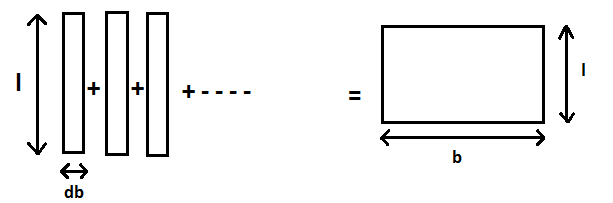
As you can see if we integrate the area of the strip from \(x = 0\) to \(x = b\)we get the area of the rectangle.
\[Area{\text{ of rectangle = }}\int\limits_0^b {ldb} \]
As l does not depend on b we can bring it out.
\[Area{\text{ of rectangle = l}}\int\limits_0^b {1db} \]
By basic properties of integration, we know the relation as:
\[\int {1dx = x + c} \]
By substituting this, we can write the equation as:
\[Area{\text{ of rectangle = l}}\left( x \right)_0^b\]
By substituting the limits into function, we get the equation:
\[Area{\text{ of rectangle = l}}\left( {b - 0} \right)\]
By simplifying the above equation, we can write it as:
\[Area {\text { of rectangle = lb}}\]
Given conditions in the question, can be written as follows:
The length of rectangle is given by the equation: \[l = 12m\]
The breadth of rectangle is given by the equation: \[b = 125cm\]
Area of rectangle can be found by substituting these:
\[Area = 12m \times 125cm\] . . . . . . . . . . . . . . . . . . . . (1)
We need to convert 12m into cms.
By basic knowledge of measurement we know the relation
\[1m = 100cm{\rm{ }} \Rightarrow {\rm{1cm = 0}}{\rm{.01m}}\]
By multiplying with 125 on both sides, we get the equation
\[125cm = 1.25m\]
By substituting this into equation (1) we can write it as:
\[Area = 12m \times 1.25m\]
By simplifying above we can write it as follows:
\[Area = 15{m^2}\]
The value of area in square meters is \[15{m^2}.\]
Note: Be careful while integrating generally students confuse and write l(dl) where they get a quadratic but that is for square here we write l(db) which leads to polynomial lb. Alternatively you can convert 12m into cm and find the area in \[c{m^2}\] at last divided by 10000 to get value in \[{m^2}\]. Anyways you get the same result.
Complete step-by-step answer:
Rectangle: In Euclidean plane geometry, a rectangle is a quadrilateral with 4 right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal. It can also be defined as a parallelogram containing a right angle. It is a two-dimensional shape.
Besides the above definition we can also define the rectangle as a combination of strips of breadth db upto b each of length l.
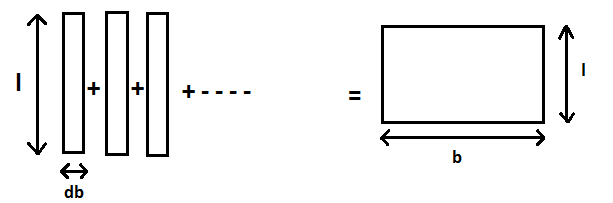
As you can see if we integrate the area of the strip from \(x = 0\) to \(x = b\)we get the area of the rectangle.
\[Area{\text{ of rectangle = }}\int\limits_0^b {ldb} \]
As l does not depend on b we can bring it out.
\[Area{\text{ of rectangle = l}}\int\limits_0^b {1db} \]
By basic properties of integration, we know the relation as:
\[\int {1dx = x + c} \]
By substituting this, we can write the equation as:
\[Area{\text{ of rectangle = l}}\left( x \right)_0^b\]
By substituting the limits into function, we get the equation:
\[Area{\text{ of rectangle = l}}\left( {b - 0} \right)\]
By simplifying the above equation, we can write it as:
\[Area {\text { of rectangle = lb}}\]
Given conditions in the question, can be written as follows:
The length of rectangle is given by the equation: \[l = 12m\]
The breadth of rectangle is given by the equation: \[b = 125cm\]
Area of rectangle can be found by substituting these:
\[Area = 12m \times 125cm\] . . . . . . . . . . . . . . . . . . . . (1)
We need to convert 12m into cms.
By basic knowledge of measurement we know the relation
\[1m = 100cm{\rm{ }} \Rightarrow {\rm{1cm = 0}}{\rm{.01m}}\]
By multiplying with 125 on both sides, we get the equation
\[125cm = 1.25m\]
By substituting this into equation (1) we can write it as:
\[Area = 12m \times 1.25m\]
By simplifying above we can write it as follows:
\[Area = 15{m^2}\]
The value of area in square meters is \[15{m^2}.\]
Note: Be careful while integrating generally students confuse and write l(dl) where they get a quadratic but that is for square here we write l(db) which leads to polynomial lb. Alternatively you can convert 12m into cm and find the area in \[c{m^2}\] at last divided by 10000 to get value in \[{m^2}\]. Anyways you get the same result.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




