Question

Find the square of the following number using the diagonal method: 98

Answer 1

Hint: We will understand the diagonal method for finding the square of a number. Then we will make the figure that will be described in the method. The figure is a square with a diagonal. We will put the digits of the given number in their designated places. Then we will do some multiplication and addition to obtain the square of the given number.

Complete step by step answer:
The diagonal method for finding the square of a number is described as follows,
(i) We form a square block having the rows and columns equal to the digit of the number.
(ii) We divide these smaller squares using diagonals and label the rows and columns with the digits of the number.
(iii) Then we multiply each row label with each column label and write the product in the smaller squares such that the tens digit is above the diagonal and the units digit is below the diagonal.
(iv) Then we add the digits in the sections created by the diagonals starting from the bottom right, and carry over the tens place digit (if any) to the section above it.
The number obtained at the end of this method is the square of the given number.
The given number is 98. It has two digits, so our block looks like the following,

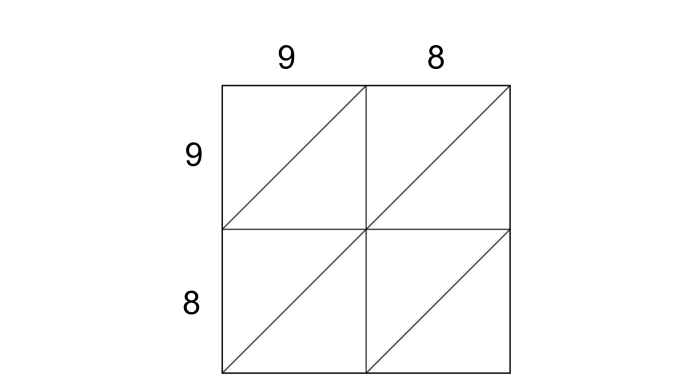
Now, performing the multiplications, we get the following,

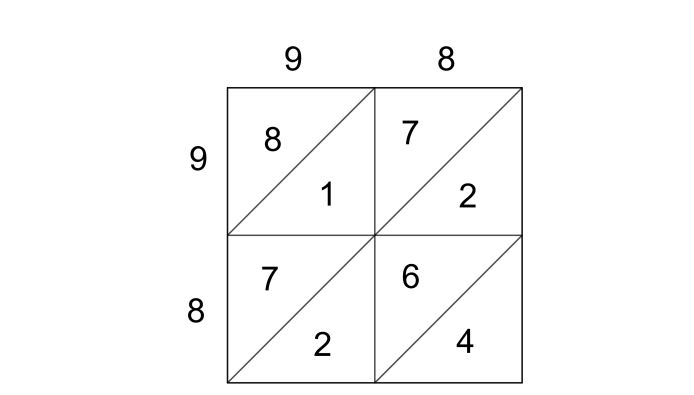
Next, we have to add the digits in the diagonal sections starting from the right bottom and carry over the tens place digit, if there is any, to the next section.
So, we get the units place as 4, since it is a single digit. Then in the second section, the addition is $2+6+2=10$. So we get the tens place as 0 and we carry over the 1 to the next section. Then we have $1+7+1+7=16$. So, the hundreds place digit is 6 and we carry over the 1 to the next section. Next, we have $1+8=9$. So, 9 is the thousand place digit. Hence, the number obtained as the square of 98 is 9604.

Note:
It is important to understand the steps of a method. The best way to understand a method is by using examples. There are many methods and tricks for different concepts. The diagonal method is for finding the square of a number. This method also works for three-digit numbers. The tricky part is to remember to start from the right bottom section while adding and carrying over the tens place digit, if any, to the next section without fail.