Question

Find the square root of 3249 by Division method.

Answer 1

Hint: Group the given digit in pairs of two unit’s place. For the 1^st period divide it with a square number less than or equal to it. The number becomes divisor. Now, to solve the rest find the product such that the digits are equal and subtract it. You should get the remainder as zero.

Complete step-by-step answer:
To find the square root of a perfect square by using the long division method is easy when the numbers are very large. We have been asked to find the square root of the number 3249.
Let us group the digits in pairs, starting with the digit in the unit’s place. Each pair and the remaining digits are called a period. Now according to this the pairs are $\overline{32}\overline{49}$ , it is represented by a bar on top of the numbers.
Now, let us think of the largest number whose square is equal to or just less than the first period. Take this number as the divisor and also the quotient. Here, 32 is the first period only ${{5}^{2}}=25$ is less than 32. Thus, divide 32 by 25 and quotient will be 5.
Now subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. This becomes the new dividend.
Now, the new divisor is obtained by taking two times the quotient and annexing with it is a suitable digit, which is also taken as the next digit of the quotient chosen in such a way that the product of the new divisor and the digit is equal to or just less than the new dividend.

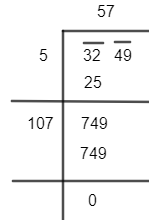
$\because 107\times 7=749$
Thus, we found square root of 3249 $=$ 57

Note: You can also find square roots by prime factorization method.

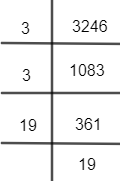
$\therefore 3249=3\times 3\times 19\times 19$
$={{3}^{2}}\times {{19}^{2}}$
$\therefore \sqrt{3249}=\sqrt{{{3}^{2}}\times {{19}^{2}}}=3\times 19=57$