Question

How can I find the square root of a number using factor trees?

Answer 1

Hint: In order to find the solution to this question that is to find the square root of a number using factor trees, there are 3 steps which we have to follow:
1). Find all prime factors of the radicand i.e. the number of which we want a square root.
2). Pull out each number that appears in a group of 2. (i.e. repeated 2 numbers)
3). Multiply those repeated numbers.
Then finally we will get the square root of a number.

Complete step-by-step solution:
For example, suppose we want to find the square root of $\sqrt{81}$ using factor trees.
Here as we can see that 81 is a radicand.
So now we will start solving the problem by:
First we will find out prime factors of the radicand that is $81$ so we will get:
 $\sqrt{81}=\sqrt{3\times 27}$

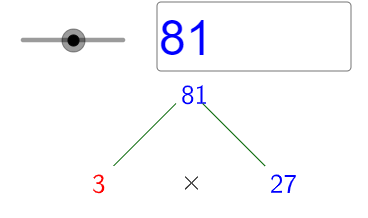
As we can see, we can further simplify this radicand that we have $27$ as a radicand and thus we can further factorize, so we get:
$\sqrt{81}=\sqrt{3\times 27}=\sqrt{3\times 3\times 9}$

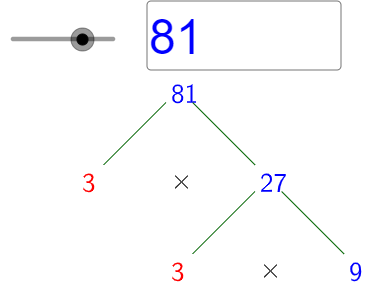
Now we are getting 9 as a radicand which can be further factorize, so we get:
$\begin{align}
  & \sqrt{81}=\sqrt{3\times 27}=\sqrt{3\times 3\times 9} \\
 & =\sqrt{3\times 3\times 3\times 3} \\
\end{align}$

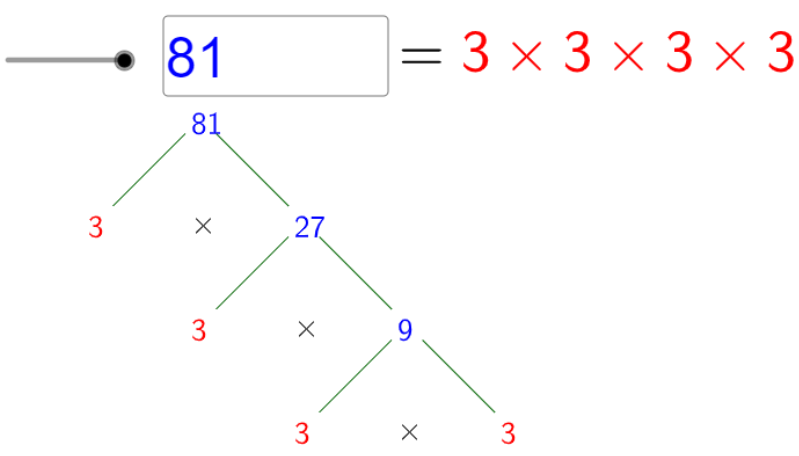
Now as we can see that the numbers cannot be factorized and so we will proceed to step 2 that is we will pull out each number that has repeated itself. So we get:
 \[\sqrt{81}=\sqrt{\underline{3\times 3}\times \underline{3\times 3}}\]
Now on step 3, so by multiplying these numbers we get:
\[=3\times 3\]
$=9$
That is the answer, therefore the square root of $\sqrt{81}$ is $9$.

Note: A square root is a factor of a number that when multiplied to itself gives us the original number. Square root is denoted by \[\sqrt{{}}\] sign.
For example, square root of $\sqrt{9}$ is $3$ or $-3$
We have to simplify square roots to reduce square roots when a perfect square doesn’t exist.