Question

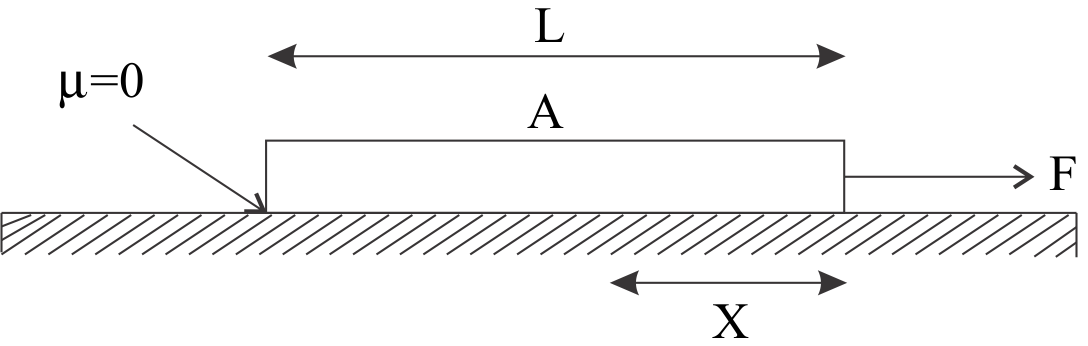
Find the tension in rope at section A, at distance x from a right end.

Answer 1

Hint: In this type of situation, force applied on the body is uniformly distributed all over the length of the rope and all over the mass of the rope. So, we can use this result to find the tension or the total force, acting on the remaining part (part of rope that is in the left of point $A$ ) of the rope.

Complete step by step solution:
Since, the force is uniformly distributed over the mass of the rope. So the tension action at point $A$ will be the total force acting on the left part of the rope from point $A$ because this point will be pulling it’s left part.
So, Let the total mass of the rope be $M$
And length of rope is $L$
So mass per unit length, $\lambda = \dfrac{M}{L}$
Now, let mass of left part of rope from point $A$ be $m$ and it’s length is $L - x$ , so,
$m = \lambda \left( {L - x} \right)$
This is equivalent to,
$m = \dfrac{M}{L}\left( {L - x} \right)$
On simplifying this, we get,
$m = M\left( {1 - \dfrac{x}{L}} \right)$ ----------(1)
Now, acceleration of the rope $a$ will be the acceleration of all points of rope which is equal to,
$a = \dfrac{F}{M}$ (because ${\text{force = mass }} \times {\text{ acceleration}}$ )
So, tension $T$ at point $A$ will be the force acting on left part of the rope from point $A$ , so,
$T = ma$
Where $m = M\left( {1 - \dfrac{x}{L}} \right)$ from equation one and $a = \dfrac{F}{M}$ ,
Using these values in expression of tension, we get,
$T = M\left( {1 - \dfrac{x}{L}} \right)\dfrac{F}{M}$
On simplifying this, we get,
$T = F\left( {1 - \dfrac{x}{L}} \right)$

So tension $T$ at point $A$ is $T = F\left( {1 - \dfrac{x}{L}} \right)$.

Note: We could say that force is uniformly distributed over the mass and length and we got equation $a = \dfrac{F}{M}$ because there was no friction. If friction would present, then it’s force would also have some contribution in the expression of acceleration and the answer would be different.