Question

Find the time period of oscillations of a torsional pendulum, if the torsional constant of the wire is $k = 10{\pi ^2}{\text{J}}/{\text{rad}}$. The moment of inertia of the rigid body is $10{\text{ }}Kg{m^2}$ about the axis of rotation.
A. 2 sec
B. 4 sec
C. 16 sec
D. 8 sec

Answer 1

Hint: A torsional pendulum is a pendulum that performs angular simple harmonic motion. In this type of pendulum the linear displacement is replaced by angular displacement. So, using the formula for the time period of the pendulum given below we can solve for the required solution.

Formula Used:
Time Period of Torsional Pendulum, $T = 2\pi \sqrt {\dfrac{I}{k}} $
where
$\eqalign{
  & I{\text{ is the moment of inertia of the system,}} \cr
  & {\text{k is torsional constant}} \cr} $

Complete step by step answer:
A body which is free to rotate about a given axis can make angular oscillations. The angular oscillations are called angular harmonic motion. The pendulum performing such oscillations is known as the Torsional pendulum. In this pendulum the restoring force is torque.
If the angular displacement of the body at an instant is $\theta $, the resultant torque acting on the body in angular simple harmonic motion should be
$\tau = - k\theta $

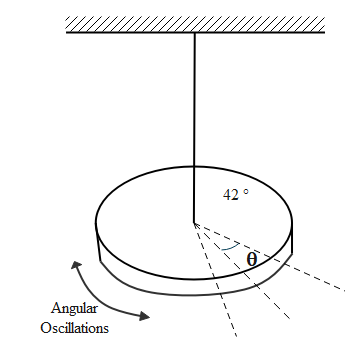
If the moment of inertia is $I$, the angular acceleration is
$\alpha = \dfrac{\tau }{I} = \dfrac{{ - k}}{I}\theta $
or,
$\eqalign{
  & \dfrac{{{d^2}\theta }}{{d{t^2}}} = - {\omega ^2}\theta \cr
  & {\text{where }}\omega {\text{ = }}\sqrt {k{I^{ - 1}}} \cr} $
The time period of the oscillation is
$T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{I}{k}} \cdots \cdots \cdots \left( 1 \right)$
Given:
Moment of inertia of rigid body, $I = 10{\text{ }}Kg{m^2}$
Torsional constant of the wire, $k = 10{\pi ^2}{\text{J}}/{\text{rad}}$
Substituting the given values in equation (1), we get:
$\eqalign{
  & T = 2\pi \sqrt {\dfrac{I}{k}} \cr
  & \Rightarrow T = 2\pi \sqrt {\dfrac{{10}}{{10{\pi ^2}}}} \cr
  & \Rightarrow T = 2\sec \cr} $
Therefore, the correct option is A. i.e., 2 seconds.

Note: In a torsion pendulum, the pendulum tends to perform rotational motion about the vertical axis of the wire, which results in the twisting of the wire rather than swinging like a normal pendulum. The force which twists the pendulum keeps reversing its direction to maintain equilibrium. Thus this pendulum also follows the necessary condition for SHM that the acceleration is opposite in direction to the displacement.