
Find the total kinetic energy of ring by analyzing the figures shown
A) $\dfrac{3}{2}M\omega _0^2\left( {R - r} \right)$
B) $\dfrac{1}{2}M\omega _0^2\left( {R - r} \right)$
C) $M\omega _0^2{\left( {R - r} \right)^2}$
D) $M\omega _0^2{R^2}$
Answer
233.4k+ views
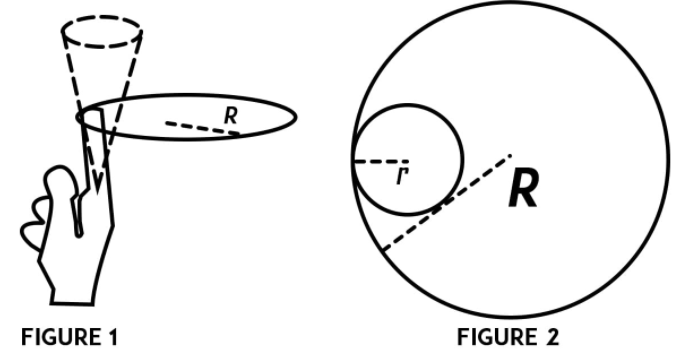
Hint: From the figure 2 given in the question we can see that the centre of mass of the ring moves in a circle of radius $R - r$.
The kinetic energy due to translation is given by the equation
\[{K_T} = \dfrac{1}{2}M{v^2}\]
Where, $M$ is the mass of the ring and $v$ is the linear velocity
let ${\omega _0}$ be the angular velocity of the centre of mass of the ring.
We know that
$\omega = \dfrac{v}{r}$
That is, $v = \omega r$.
Therefore, \[{K_T} = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2}\]
The kinetic energy due to rotation is given by the equation
${K_R} = \dfrac{1}{2}I\omega _0^2$
Where, the moment of inertia of the ring $I = M{R^2}$.
Total kinetic energy is the sum of both kinetic energy due to translation and rotation.
$K = {K_T} + {K_R}$
Complete step by step solution:
Let the mass of the ring be $M$ and its radius be $R$and $v$ be the linear velocity and let ${\omega _0}$ be the angular velocity of the centre of mass of the ring.
From the figure 2 given in the question we can see that the centre of mass of the ring moves in a circle of radius $R - r$.
The kinetic energy due to translation is given by the equation
\[{K_T} = \dfrac{1}{2}M{v^2}\]
We know that
$\omega = \dfrac{v}{r}$
That is, $v = \omega r$.
Now let us substitute all these values in the equation for translational kinetic energy.
\[{K_T} = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2}\]
The kinetic energy due to rotation is given by the equation
${K_R} = \dfrac{1}{2}I\omega _0^2$
Where, the moment of inertia of the ring $I = M{R^2}$.
Therefore,
${K_R} = \dfrac{1}{2}M{R^2}\omega _0^2$
Total kinetic energy is the sum of both kinetic energy due to translation and rotation.
$K = {K_T} + {K_R}$
Substitute the values of kinetic energy due to translation and rotation. Then, we get
$K = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2} + \dfrac{1}{2}M{R^2}\omega _0^2$
$ \Rightarrow K = \dfrac{1}{2}M\omega _0^2{R^2}{\left( {1 - \dfrac{r}{R}} \right)^2} + \dfrac{1}{2}M{R^2}\omega _0^2$
Since, $r < < R$
We can consider the term $\dfrac{r}{R} = 0$
$ \Rightarrow K = \dfrac{1}{2}M\omega _0^2{R^2} + \dfrac{1}{2}M{R^2}\omega _0^2 = M{R^2}\omega _0^2$
So, the correct answer is option (D).
Note: While substituting for the radius in the equation for kinetic energy due to translation, don't substitute the radius of the ring $R$. We need to consider the circle in which centre of mass moves. From the figure we can see that the radius of this circle will be $R - r$. Similarly, the angular velocity ${\omega _0}$ that we considered is the angular velocity of the centre of mass.
The kinetic energy due to translation is given by the equation
\[{K_T} = \dfrac{1}{2}M{v^2}\]
Where, $M$ is the mass of the ring and $v$ is the linear velocity
let ${\omega _0}$ be the angular velocity of the centre of mass of the ring.
We know that
$\omega = \dfrac{v}{r}$
That is, $v = \omega r$.
Therefore, \[{K_T} = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2}\]
The kinetic energy due to rotation is given by the equation
${K_R} = \dfrac{1}{2}I\omega _0^2$
Where, the moment of inertia of the ring $I = M{R^2}$.
Total kinetic energy is the sum of both kinetic energy due to translation and rotation.
$K = {K_T} + {K_R}$
Complete step by step solution:
Let the mass of the ring be $M$ and its radius be $R$and $v$ be the linear velocity and let ${\omega _0}$ be the angular velocity of the centre of mass of the ring.
From the figure 2 given in the question we can see that the centre of mass of the ring moves in a circle of radius $R - r$.
The kinetic energy due to translation is given by the equation
\[{K_T} = \dfrac{1}{2}M{v^2}\]
We know that
$\omega = \dfrac{v}{r}$
That is, $v = \omega r$.
Now let us substitute all these values in the equation for translational kinetic energy.
\[{K_T} = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2}\]
The kinetic energy due to rotation is given by the equation
${K_R} = \dfrac{1}{2}I\omega _0^2$
Where, the moment of inertia of the ring $I = M{R^2}$.
Therefore,
${K_R} = \dfrac{1}{2}M{R^2}\omega _0^2$
Total kinetic energy is the sum of both kinetic energy due to translation and rotation.
$K = {K_T} + {K_R}$
Substitute the values of kinetic energy due to translation and rotation. Then, we get
$K = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2} + \dfrac{1}{2}M{R^2}\omega _0^2$
$ \Rightarrow K = \dfrac{1}{2}M\omega _0^2{R^2}{\left( {1 - \dfrac{r}{R}} \right)^2} + \dfrac{1}{2}M{R^2}\omega _0^2$
Since, $r < < R$
We can consider the term $\dfrac{r}{R} = 0$
$ \Rightarrow K = \dfrac{1}{2}M\omega _0^2{R^2} + \dfrac{1}{2}M{R^2}\omega _0^2 = M{R^2}\omega _0^2$
So, the correct answer is option (D).
Note: While substituting for the radius in the equation for kinetic energy due to translation, don't substitute the radius of the ring $R$. We need to consider the circle in which centre of mass moves. From the figure we can see that the radius of this circle will be $R - r$. Similarly, the angular velocity ${\omega _0}$ that we considered is the angular velocity of the centre of mass.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




