Question

Find the value of \[{{R}_{L}}\] for maximum power transfer in the circuit and find the maximum power.

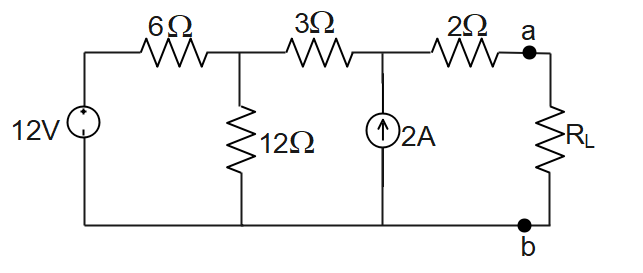
Answer 1

Hint: Maximum power transfer theorem is particularly useful for analyzing communication networks because in communication engineering it is usually desirable to deliver maximum power to a load. Electronic amplifiers in radio and television receivers are so designed to do this as it does not matter that an equal amount of power is lost in the process.

Complete step-by-step solution:
 Maximum power transfer theorem is stated as follows:
A resistive load, served through a resistive network, will abstract maximum power when the load resistance value is the same as the resistance “viewed by the load as it looks back into the network “.This is called the output resistance of the network or the resistance presented to the output terminals by the network. It is the resistance we called ${{R}_{T}}$ in explaining Thevenin’s theorem. The load resistance ${{R}_{L}}$ will draw maximum power drawn will be equal to ${{R}_{T}}$ i.e.,${{R}_{L}}={{R}_{T}}$ and the maximum power drawn will be equal to $\dfrac{{{V}_{OC}}^{2}}{4{{R}_{L}}}$ where ${{V}_{OC}}$ is the open-circuit voltage at the terminals from which ${{R}_{L}}$has been disconnected.
To find ${{R}_{T}}$in the given circuit short circuit the voltage source and open circuit the current source.

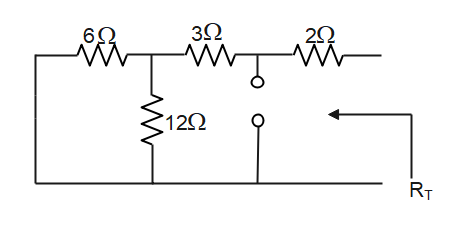
$\begin{align}
  & {{R}_{T}}=(\dfrac{6\times 12}{6+12})+3 \\
 & {{R}_{T}}=4+3=7\Omega \\
\end{align}$
To find ${{V}_{OC}}$ remove the load resistor

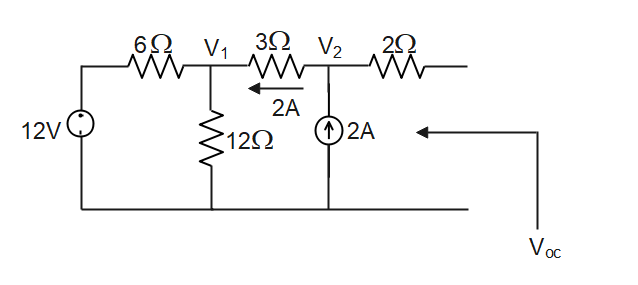
${{V}_{OC}}={{V}_{2}}$
Apply KCL to the circuit
$\begin{align}
  & \dfrac{{{V}_{1}}-12}{6}+\dfrac{{{V}_{1}}}{12}=2 \\
 & \Rightarrow 0.166{{V}_{1}}-2+0.083{{V}_{1}}=2 \\
 & \Rightarrow 0.2493{{V}_{1}}=4 \\
 & {{V}_{1}}=\dfrac{4}{0.2493}=16V \\
\end{align}$
$\begin{align}
  & {{V}_{2}}={{V}_{1}}+IR \\
 & {{V}_{2}}=16+(2)3 \\
 & {{V}_{2}}=22V \\
\end{align}$
${{V}_{OC}}=22V$
Maximum power transfer will happen when ${{R}_{L}}={{R}_{T}}$
From maximum power transfer theorem
${{P}_{Max}}=\dfrac{\dfrac{1}{4}{{V}_{OC}}^{2}}{{{R}_{L}}}$
After substituting
$\begin{align}
  & {{P}_{Max}}=\dfrac{\dfrac{1}{4}{{(22)}^{2}}}{7} \\
 & {{P}_{Max}}=17.28watt \\
\end{align}$
The maximum power is equal to 17.28watt.

Note: Students similarly for a current source the power transferred will be maximum when load conductance is equal to source conductance and maximum power transferred is ${{P}_{Max}}=\dfrac{\dfrac{1}{4}{{V}_{OC}}^{2}}{{{R}_{L}}}$. It is important to make maximum use of power available for driving a loudspeaker.SI unit of power is watt (W).