Question

Find the value of ${{\sec }^{-1}}\left( \sec \dfrac{8\pi }{5} \right)$

Answer 1

Hint:Use the fact that the range of the function ${{\sec }^{-1}}x$ is $\left[ 0,\pi \right]-\left\{ \dfrac{\pi }{2} \right\}$. Put $y={{\sec }^{-1}}\left( \sec \dfrac{8\pi }{5} \right)$ and use the fact that if $y={{\sec }^{-1}}x$, then $x=\sec y$. Use the fact that if $\cos x=\cos y$, then $x=2n\pi \pm y,n\in \mathbb{Z}$. Hence find the value of y and hence find the value of ${{\sec }^{-1}}\sec \dfrac{8\pi }{5}$

Complete step by step answer:
Before solving the above question, we must understand how ${{\sec }^{-1}}x$ is defined even when $\sec x$ is not one-one.
We know that sec x is a periodic function.
Let us draw the graph of sec x

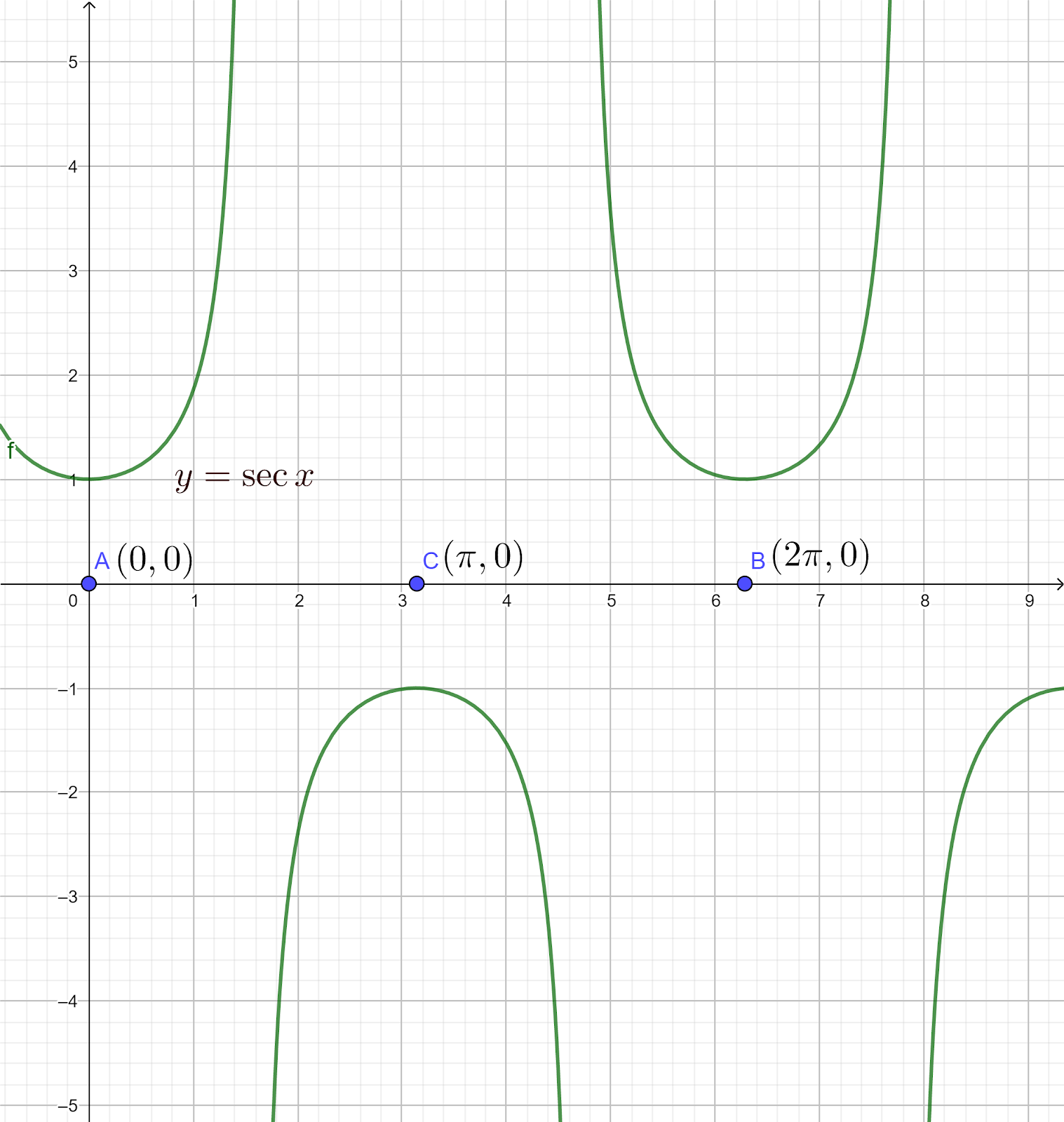
As is evident from the graph secx is a repeated chunk of the graph of secx within the interval $\left[ A,B \right]-\left\{ \dfrac{\pi }{2},\dfrac{3\pi }{2} \right\}$ , and it attains all its possible values in the interval $\left[ A,C \right]-\left\{ \dfrac{\pi }{2} \right\}$.
Here $A=0,B=2\pi $ and $C=\pi $
Hence if we consider secx in the interval \[\left[ A,C \right]-\left\{ \dfrac{\pi }{2} \right\}\], we will lose no value attained by secx, and at the same time, secx will be one-one and onto.
Hence ${{\sec }^{-1}}x$ is defined over the Domain $\left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$, with codomain $\left[ 0,\pi \right]-\left\{ \dfrac{\pi }{2} \right\}$ as in the Domain $\left[ 0,\pi \right]-\left\{ \dfrac{\pi }{2} \right\}$, secx is one-one and $\text{Range}\left( \sec x \right)=\left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$.
Now since ${{\sec }^{-1}}x$ is the inverse of secx it satisfies the fact that if $y={{\sec }^{-1}}x$, then $\sec y=x$.
So let $y={{\sec }^{-1}}\sec \dfrac{8\pi }{5}$
Hence we have $\sec y=\sec \dfrac{8\pi }{5},y\in \left[ 0,\pi \right]-\left\{ \dfrac{\pi }{2} \right\}$
Taking reciprocals on both sides, we get
$\dfrac{1}{\sec y}=\dfrac{1}{\sec \dfrac{8\pi }{5}}$
We know that $\cos \theta =\dfrac{1}{\sec \theta }$.
Hence, we have
$\cos y=\cos \dfrac{8\pi }{5}$
We know that if $\cos x=\cos y$, then
Hence, we have
$y=2n\pi \pm \dfrac{8\pi }{5}$
Since $y\in \left[ 0,\pi \right]-\left\{ \dfrac{\pi }{2} \right\}$, we put n = 1 and take the negative sign.
Hence, we have
$y=2\pi -\dfrac{8\pi }{5}=\dfrac{2\pi }{5}$
Hence, we have
${{\sec }^{-1}}\sec \dfrac{8\pi }{5}=\dfrac{2\pi }{5}$
Hence option [a] is correct.

Note:
Alternative solution:
We know that ${{\sec }^{-1}}x={{\cos }^{-1}}\dfrac{1}{x}$. Hence, we have
${{\sec }^{-1}}\sec \dfrac{8\pi }{5}={{\cos }^{-1}}\cos \dfrac{8\pi }{5}$
We know that
${{\cos }^{-1}}\cos x=\left\{ \begin{matrix}
   \vdots \\
   2\pi +x,x\in \left[ -\pi ,0 \right] \\
   x,x\in \left[ 0,\pi \right] \\
   2\pi -x,x\in \left[ \pi ,2\pi \right] \\
   \vdots \\
\end{matrix} \right.$
Since $\dfrac{8\pi }{5}\in \left[ \pi ,2\pi \right]$, we have
${{\cos }^{-1}}\cos \dfrac{8\pi }{5}=2\pi -\dfrac{8\pi }{5}=\dfrac{2\pi }{5}$
Hence option [a] is correct.