Question

Find the value of \[\sqrt {3.5} \] geometrically.

Answer 1

Hint: Here we will follow some basic steps to draw the required number. Below are the steps that need to follow:
To mark any number \[\sqrt x \] on the number line, first of all, we will draw a line \[{\text{AB}}\] of \[x\] units.
After extending that line to \[1\] unit till point \[{\text{C}}\], we will find the midpoint of that particular line \[{\text{AC}}\] which is \[x + 1\] units, and marking it as point \[{\text{E}}\]
We will draw a semicircle after that taking \[{\text{E}}\] as a Centre point and \[{\text{AC}}\] as diameter.
After that, we will draw a perpendicular line from the point \[{\text{B}}\], which cuts the semicircle at the point \[{\text{D}}\].
So, \[{\text{BD}}\] is required \[\sqrt x \].

Complete step-by-step solution:
Step 1: For finding the value of
\[\sqrt {3.5} \] first of all we will draw a line of
\[3.5\] the unit as shown below:

Step 2: Now, by extending the line
\[{\text{PQ}}\] to \[1\] the unit, we get:

Step 3: Now we will find the midpoint of
\[{\text{PR = 4}}{\text{.5 unit}}\], which is a point
\[{\text{S}}\], by using the scale or by drawing the bisector of that line such that \[{\text{PS = SR = 2}}{\text{.25 unit}}\], as shown below:

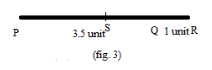
Step 4: Now, by drawing a semicircle taking
\[{\text{S}}\] as a Centre point and \[{\text{PR}}\] as diameter, we get the below figure:

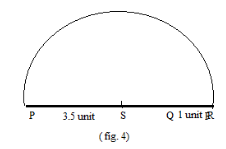
Step 5: Now by drawing a perpendicular line from the point
\[{\text{Q}}\] which cuts the semi-circle at the point \[{\text{T}}\], we get the below figure:

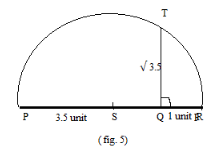
Step 6: Now, the line
\[{\text{QT}}\] is our required line of \[\sqrt {3.5} \] the unit.
Answer/Conclusion:
\[\because \] Our required figure is as below:

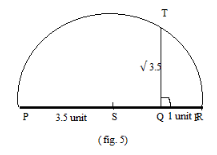
Note: Students can follow the below proof for calculating the value of any number
\[\sqrt x \] geometrically for their better understanding:
First of all, we will draw a line \[{\text{AB}}\] of \[x\] units. After extending that line to \[1\] unit till point \[{\text{C}}\], we will find the midpoint of that particular line \[{\text{AC}}\] which is \[x + 1\] units and marking it as a point \[{\text{E}}\]. We will draw a semicircle after that taking \[{\text{E}}\] as a Centre point and \[{\text{AC}}\] as diameter. After that we will draw a perpendicular line from the point \[{\text{B}}\], which cuts the semicircle at the point \[{\text{D}}\] as shown in the below diagram:

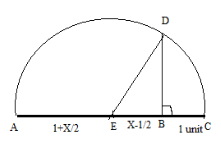
In the above diagram, we know that \[{\text{AC = }}x + 1\]. Because \[{\text{E}}\] is the midpoint of the line \[{\text{AC}}\] then, \[{\text{AE = }}\left( {\dfrac{{x + 1}}{2}} \right)\] and similarly we will find the value of \[{\text{EB}}\] as shown below:
\[ \Rightarrow {\text{EB = AB - AE}}\]
By substituting the value of \[{\text{AE = }}\left( {\dfrac{{x + 1}}{2}} \right)\] and \[{\text{AB = }}x\] in the above expression, we get:
\[ \Rightarrow {\text{EB = }}x{\text{ - }}\left( {\dfrac{{x + 1}}{2}} \right)\]
By simplifying the above expression, we get:
\[ \Rightarrow {\text{EB = }}\left( {\dfrac{{x - 1}}{2}} \right)\]
Now, by using Pythagoras theorem \[\Delta {\text{EDB}}\], we get:
\[ \Rightarrow {\left( {{\text{ED}}} \right)^2} = {\left( {{\text{EB}}} \right)^2} + {\left( {{\text{BD}}} \right)^2}\]
By substituting the values of \[{\text{EB = }}\left( {\dfrac{{x - 1}}{2}} \right)\] and \[{\text{ED = }}\left( {\dfrac{{x + 1}}{2}} \right)\], because \[{\text{ED}}\]is the radius of the circle, we get:
\[ \Rightarrow {\left( {\dfrac{{1 + x}}{2}} \right)^2} = {\left( {\dfrac{{x - 1}}{2}} \right)^2} + {\left( {{\text{BD}}} \right)^2}\]
By bringing \[{\left( {\dfrac{{x - 1}}{2}} \right)^2}\] into the LHS side of the expression, we get:
\[ \Rightarrow {\left( {\dfrac{{1 + x}}{2}} \right)^2} - {\left( {\dfrac{{x - 1}}{2}} \right)^2} = {\left( {{\text{BD}}} \right)^2}\]
By subtracting into the LHS side of the above expression we get:
\[ \Rightarrow \dfrac{{1 + {x^2} + 2x - {x^2} - 1 + 2x}}{4} = {\left( {{\text{BD}}} \right)^2}\]
By simplifying the numerator of the term \[\dfrac{{1 + {x^2} + 2x - {x^2} - 1 + 2x}}{4}\] , we get:
\[ \Rightarrow \dfrac{{4x}}{4} = {\left( {{\text{BD}}} \right)^2}\]
By eliminating \[4\] from the LHS side of the expression we get:
\[ \Rightarrow x = {\left( {{\text{BD}}} \right)^2}\]
By taking root on both sides of the above expression, we get:
\[ \Rightarrow \sqrt x = {\text{BD}}\]
Hence proved.