Question

Find the value of $\tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan 47{}^\circ \tan 81{}^\circ $.

Answer 1

Hint: This kind of problem observes the values of angles. If there are any angles for which their sum is equal to $90{}^\circ $ or $180{}^\circ $ etc. Then convert either one of those trigonometric ratios into an anti-trigonometric ratio. Then both get canceled and the result will remain. You will get the clarity once we start the problem.

Complete step by step answer:
Given that $\tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan 47{}^\circ \tan 81{}^\circ $
Here we have $9{}^\circ +81{}^\circ =90{}^\circ $ and $43{}^\circ +47{}^\circ =90{}^\circ $ so we will convert $\tan 9{}^\circ $ or $\tan 81{}^\circ $ to $\cot x$ and $\tan 43{}^\circ $ or $\tan 47{}^\circ $ to $\cot $.so
$\Rightarrow \tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan 47{}^\circ \tan 81{}^\circ =\tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan \left( 90{}^\circ -43{}^\circ \right)\tan \left( 90{}^\circ -9{}^\circ \right)$
We know that $\tan \left( 90{}^\circ -\theta \right)=\cot \theta $ then
$\Rightarrow \tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan 47{}^\circ \tan 81{}^\circ =\tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \cot 43{}^\circ \cot 9{}^\circ $
We know that $\cot x=\dfrac{1}{\tan x}$, then
$\begin{align}
  &\Rightarrow \tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan 47{}^\circ \tan 81{}^\circ =\left( \tan 9{}^\circ \times \dfrac{1}{\tan 9{}^\circ } \right)\left( \tan 43{}^\circ \times \dfrac{1}{\tan 43{}^\circ } \right)\tan 60{}^\circ \\
 & =1\left( 1 \right)\tan 60{}^\circ
\end{align}$
Substituting the value of $\tan 60{}^\circ =\sqrt{3}$ in the above equation, then
$\Rightarrow \tan 9{}^\circ \tan 43{}^\circ \tan 60{}^\circ \tan 47{}^\circ \tan 81{}^\circ =\sqrt{3}$

Note: While converting the trigonometric ratios we need to keep an eye on the sign conventions. We generally follow the below diagram to find the sign convention for the trigonometric ratios of different angles in different quadrants.

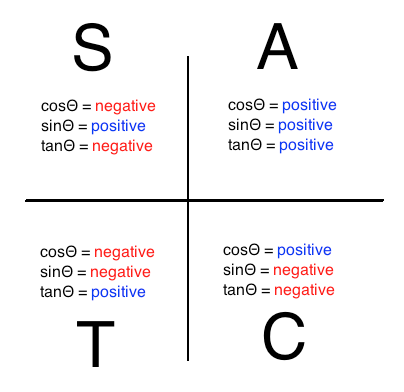
For the even angles the trigonometric ratios change to their respective inverse trigonometric ratio.