Question

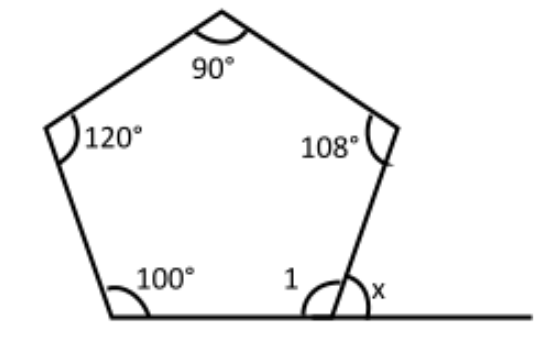
Find the value of $x$ in the given figure.

Answer 1

Hint: Using polygon formula to find missing angle and then find.This polygon is a pentagon and we find the value of $\angle 1$ further, we will find the value of x.

Formula used: Sum of angles in a pentagon is \[540^\circ \] i.e. $\angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 = {540^o}$.

Complete step by step answer:
(1) Given angles of pentagon are: \[108^\circ ,90^\circ ,120^\circ ,100^\circ ,\angle 1\]
We know sum of all five angles of a pentagon is \[540^\circ .\]
(2) Calculating sum of all five angles \[108^\circ + 90^\circ + 120^\circ + 100^\circ + \angle 1 = 540^\circ \]
\[ \Rightarrow 418^\circ + \angle 1 = 540^\circ \]
\[ \Rightarrow \angle 1{\text{ = }}540^\circ -418^\circ \]
\[\therefore \angle 1{\text{ }} = {\text{ }}122^\circ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ldots \ldots \left( i \right)\]
 (3) From the figure, we see that $\angle 1$ and $x$ are linear pairs.
from equation (i)
\[\therefore \angle 1 + x = 180^\circ \]
\[ \Rightarrow \,\,122^\circ + x = 180^\circ \]
\[ \Rightarrow x = 180^\circ - 122^\circ \]
\[\therefore x = 58^\circ \]
Therefore, the value of \[x\] is \[58^\circ \] .

Note: Sum of angles of every polygon is fixed and it depends upon the number of sides of the polygon. In geometry, a pentagon is a five sided polygon with five straight sides and five interior angles that sum up to \[540^\circ \]. A pentagon shape is a plane figure, or flat (two-dimensional) 5- sided geometric shape.