
Find the value of
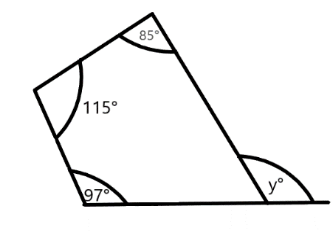

Answer
410.4k+ views
Hint: In order to find the value of y, we would be using the properties of quadrilateral and a straight line. The property of a quadrilateral states that the sum of the interior angles of a quadrilateral is equal to
Complete step by step answer:
We are given the figure of quadrilaterals. Let’s name all the corner sides of the quadrilateral is ABCD, and the respective figure obtained is:
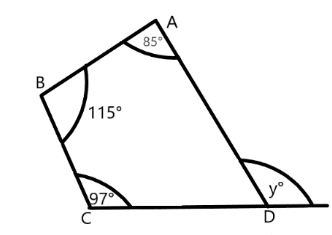
Now, we have a quadrilateral named ABCD. And, from the properties of quadrilaterals we know that the sum of all the interior angles of a quadrilateral is equal to
Substituting all the values of A, B, C and D from the figure in the above formula, we get:
Solving the above equation to obtain the value of interior angle of D, and we get:
Subtracting both the sides by
And, we obtain that the value of the interior angle D is
Now, at the point D, using the linear angle property of a straight line, we can write the equation as:
As, we know that according to the linear angle property all the angles lying at a point sum to be
Now, substituting the value of angle D from equation 1 into the equation 2, we get:
Subtracting both sides by
Therefore, the value of y is
Note:If ever given to find any value for another polygon then we can use the formula of
Complete step by step answer:
We are given the figure of quadrilaterals. Let’s name all the corner sides of the quadrilateral is ABCD, and the respective figure obtained is:

Now, we have a quadrilateral named ABCD. And, from the properties of quadrilaterals we know that the sum of all the interior angles of a quadrilateral is equal to
Substituting all the values of A, B, C and D from the figure in the above formula, we get:
Solving the above equation to obtain the value of interior angle of D, and we get:
Subtracting both the sides by
And, we obtain that the value of the interior angle D is
Now, at the point D, using the linear angle property of a straight line, we can write the equation as:
As, we know that according to the linear angle property all the angles lying at a point sum to be
Now, substituting the value of angle D from equation 1 into the equation 2, we get:
Subtracting both sides by
Therefore, the value of y is
Note:If ever given to find any value for another polygon then we can use the formula of
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

What does R mean in math class 7 maths CBSE

How many crores make 10 million class 7 maths CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE





