
Find the value of\[\sin {{120}^{\circ }}\].
A) \[\dfrac{\sqrt{3}}{2}\]
B) \[-\dfrac{\sqrt{3}}{2}\]
C) \[\dfrac{1}{2}\]
D) \[-\dfrac{1}{2}\]
Answer
512.4k+ views
Hint: Draw a unit circle and chart out the trigonometric values on each quadrant of the circle. Find the value of \[\sin {{120}^{\circ }}\] or the value of \[\sin {{120}^{\circ }}\]can be taken from the trigonometric table. Find either sine function or cosine function.
Complete step-by-step answer:
By using a unit circle we can find the value of \[\sin {{120}^{\circ }}\]. Now let us draw a cartesian plane with \[x=\cos \theta \] and \[y=\sin \theta \].
Let us draw the trigonometric table as well:
Now let us mark their values in the unit circle.
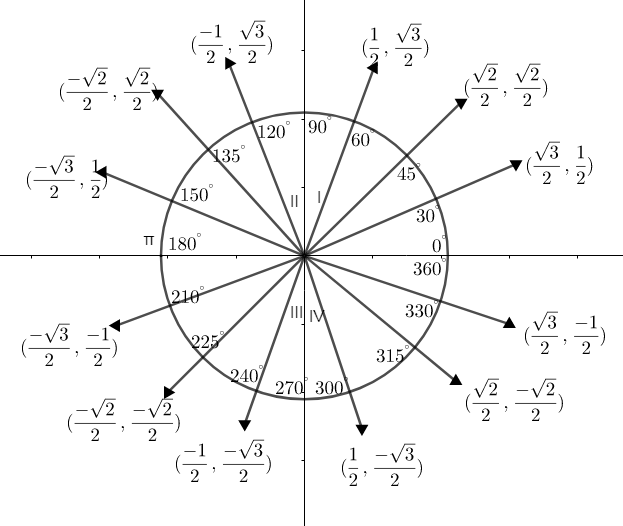
Here, \[x=\cos \theta ,y=\sin \theta \].
Eg: -\[\left( \cos {{30}^{\circ }},\sin {{30}^{\circ }} \right)=\left( x,y \right)\]
\[\left( x,y \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right)\].
In the first quadrant, the values of \[\cos \theta \] and \[\sin \theta \] are positive.
In the second quadrant, the value of \[\cos \theta \] is negative and \[\sin \theta \] is positive.
In the third quadrant, both are negative.
In the fourth quadrant, \[\cos \theta \] is positive and \[\sin \theta \] is negative.
By looking into the figure, you can find that \[\sin 60=\sin 120\].
i.e. \[\sin 60=\sin 120=\dfrac{\sqrt{3}}{2}\]
Or if we are directly taking value from the trigonometric table, we need to find the value of \[\sin {{120}^{\circ }}\] by using other angles of sin functions such as \[{{60}^{\circ }}\] and \[\sin {{180}^{\circ }}\].
We know that \[{{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}\].
We also know that the trigonometric identity:
\[\sin \left( 180-\theta \right)=\sin \theta \].
Put, \[\theta ={{120}^{\circ }}\].
\[\begin{align}
& \Rightarrow \sin \left( 180-120 \right)=\sin {{120}^{\circ }} \\
& \Rightarrow \sin {{60}^{\circ }}=\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
From the trigonometric table, find the value of \[\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
\[\therefore \]Value of \[\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\]
\[\therefore \]Option (a) is the correct answer.
Note:
We can also find the value of \[\sin {{120}^{\circ }}\] by using cosine function.
Using the trigonometry formula,
\[\sin \left( 90+\theta \right)=\cos \theta \]
Thus to find the values of \[\sin {{120}^{\circ }}\], put \[\theta ={{30}^{\circ }}\]
as, \[{{90}^{\circ }}+{{30}^{\circ }}={{120}^{\circ }}\]
\[\begin{align}
& \Rightarrow \sin \left( 90+30 \right)=\cos 30 \\
& \sin {{120}^{\circ }}=\cos {{30}^{\circ }} \\
\end{align}\]
From trigonometric table, value of \[\cos 30=\dfrac{\sqrt{3}}{2}\]
\[\therefore \sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
Complete step-by-step answer:
By using a unit circle we can find the value of \[\sin {{120}^{\circ }}\]. Now let us draw a cartesian plane with \[x=\cos \theta \] and \[y=\sin \theta \].
Let us draw the trigonometric table as well:
| sin | cos | tan | cot | sec | Cosec | |
| 0 | 0 | 1 | 0 | N.A | 1 | N.A |
| 30 | \[\dfrac{1}{2}\] | \[\dfrac{\sqrt{3}}{2}\] | \[\dfrac{1}{\sqrt{3}}\] | \[\sqrt{3}\] | \[\dfrac{2\sqrt{3}}{3}\] | 2 |
| 45 | \[\dfrac{1}{\sqrt{2}}\] | \[\dfrac{1}{\sqrt{2}}\] | 1 | 1 | \[\sqrt{2}\] | \[\sqrt{2}\] |
| 60 | \[\dfrac{\sqrt{3}}{2}\] | \[\dfrac{1}{2}\] | \[\sqrt{3}\] | \[\dfrac{\sqrt{3}}{3}\] | 2 | \[\dfrac{2\sqrt{3}}{3}\] |
| 90 | 1 | 0 | N.A | 0 | N.A | 1 |
Now let us mark their values in the unit circle.

Here, \[x=\cos \theta ,y=\sin \theta \].
Eg: -\[\left( \cos {{30}^{\circ }},\sin {{30}^{\circ }} \right)=\left( x,y \right)\]
\[\left( x,y \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right)\].
In the first quadrant, the values of \[\cos \theta \] and \[\sin \theta \] are positive.
In the second quadrant, the value of \[\cos \theta \] is negative and \[\sin \theta \] is positive.
In the third quadrant, both are negative.
In the fourth quadrant, \[\cos \theta \] is positive and \[\sin \theta \] is negative.
By looking into the figure, you can find that \[\sin 60=\sin 120\].
i.e. \[\sin 60=\sin 120=\dfrac{\sqrt{3}}{2}\]
Or if we are directly taking value from the trigonometric table, we need to find the value of \[\sin {{120}^{\circ }}\] by using other angles of sin functions such as \[{{60}^{\circ }}\] and \[\sin {{180}^{\circ }}\].
We know that \[{{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}\].
We also know that the trigonometric identity:
\[\sin \left( 180-\theta \right)=\sin \theta \].
Put, \[\theta ={{120}^{\circ }}\].
\[\begin{align}
& \Rightarrow \sin \left( 180-120 \right)=\sin {{120}^{\circ }} \\
& \Rightarrow \sin {{60}^{\circ }}=\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
From the trigonometric table, find the value of \[\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
\[\therefore \]Value of \[\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\]
\[\therefore \]Option (a) is the correct answer.
Note:
We can also find the value of \[\sin {{120}^{\circ }}\] by using cosine function.
Using the trigonometry formula,
\[\sin \left( 90+\theta \right)=\cos \theta \]
Thus to find the values of \[\sin {{120}^{\circ }}\], put \[\theta ={{30}^{\circ }}\]
as, \[{{90}^{\circ }}+{{30}^{\circ }}={{120}^{\circ }}\]
\[\begin{align}
& \Rightarrow \sin \left( 90+30 \right)=\cos 30 \\
& \sin {{120}^{\circ }}=\cos {{30}^{\circ }} \\
\end{align}\]
From trigonometric table, value of \[\cos 30=\dfrac{\sqrt{3}}{2}\]
\[\therefore \sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
What constitutes the central nervous system How are class 10 biology CBSE

What is the past participle of wear Is it worn or class 10 english CBSE

This cake is sweet that one A As sweet as B Sweeter class 10 english CBSE

Lets have a cup of tea A Havent we B Have we C Will class 10 english CBSE

What are five examples of facts and opinions class 10 english CBSE

Complete the sentence with the most appropriate word class 10 english CBSE




