Question

How do you find the vertex of the parabola with two points?

Answer 1

Hint: Firstly, write the general equation for a parabola and then write the formula for its vertex. Now substitute the coordinates and try to find the values of the unknown variables in the general equation of the parabola.

Complete step by step solution:
A parabola is a geometric curve that is equidistant from a fixed point and a fixed-line.

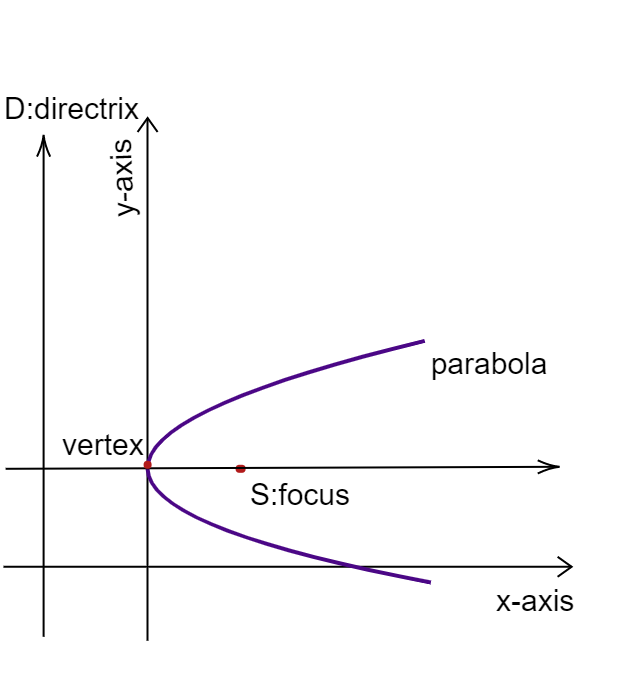
The vertex always lies midway between the Focus and the directrix of the Parabola.
The general form of a parabola is given by, $y=a{{x}^{2}}+bx+c$
The formula for finding the vertex is given by,
$\Rightarrow \dfrac{-b}{2a}$ for the x – coordinate.
So, for that, we need to find the variables a, b, c.
Since there are three unknown variables which are needed to be found out,
We require three points to find them.
We substitute all these three points and get three equations.
Let the three coordinates be, $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$
When we substitute, we get three equations.
$\Rightarrow {{y}_{1}}=a{{x}_{1}}^{2}+b{{x}_{1}}+c$
$\Rightarrow {{y}_{2}}=a{{x}_{2}}^{2}+b{{x}_{2}}+c$
$\Rightarrow {{y}_{3}}=a{{x}_{3}}^{2}+b{{x}_{3}}+c$
By solving these three equations we get, the values of the variables a, b, c.
Then we can substitute it in the general formula for a vertex and then get its values.
Given in the question that we need to find the vertex of the parabola using just two points.
It is highly impossible to find in that way.
We need a minimum requirement of three points.
When there are only two points, an infinite number of a parabola can be drawn, passing through them.
We need that one extra coordinate to find the exact parabola we are looking for.

Note: The given equation is in the form of the Parabola formula,$y=a{{x}^{2}}+bx+c$
The general equation of a parabola whose vertex is at $\left( h,k \right)$ is,
$\Rightarrow {{(x-h)}^{2}}=4a{{(y-k)}^{{}}}$
Here, $4a\;$ is the length of the latus rectum. The focal diameter of the parabola is known as the Latus rectum of the parabola which is the length of the line passing through the focus crossing the parabola.