Question

How do you find the vertex, \[x\] - intercept, \[y\] - intercept, and graph the equation \[y = - 4{x^2} + 20x - 24\]?

Answer 1

Hint:This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. We need to know the basic formula to find vertex from the given equation. Also, we need to know the basic conditions for finding\[x\]-intercept and \[y\] -intercept. We need to know how to draw a graph with the given equation. Also, we need to know the basic form of a quadratic equation.

Complete step by step solution:
The given equation is shown below,
\[y = - 4{x^2} + 20x - 24 \to \left( 1 \right)\]
The basic form of a quadratic equation is,
\[y = a{x^2} + bx + c\]
So, the value of
\[
a = - 4 \\
b = 20 \\
c = - 24 \\
\]
We know that if the value \[a\] is negative, then the parabolic shape will be in a downward position.
The basic form of the vertex is \[\left( {h,k} \right)\]. Let’s find the value of \[h\],
We know that,
\[h = \dfrac{{ - b}}{{2a}} \to \left( 2 \right)\]
By substituting the values of\[a = - 4\]and\[b = 20\]in the above equation we get,
\[
h = \dfrac{{ - 20}}{{2 \times - 4}} = \dfrac{{ - 20}}{{ - 8}} \\
h = \dfrac{5}{2} \\
\]
For finding the value of \[k\], we substitute the value of \[h\]in the equation \[\left( 1
\right)\]instead of\[x\]. So, we get
\[\left( 1 \right) \to y = - 4{x^2} + 20x - 24\]
\[
y = - 4{\left( {\dfrac{5}{2}} \right)^2} + 20\left( {\dfrac{5}{2}} \right) - 24 \\
y = - 4\left( {\dfrac{{25}}{4}} \right) + \left( {10 \times 5} \right) - 24 \\
y = - 25 + 50 - 24 \\
\]
\[y = 1\]
Take\[y\]as\[k\]
So, we get \[\left( {h,k} \right) = \left( {\dfrac{5}{2},1} \right)\]
The vertex point is \[\left( {h,k} \right) = \left( {\dfrac{5}{2},1} \right)\]
Next, we would find \[x\] and \[y\] -intercept. We know that if we want to find \[x\] -intercept, then we have to set \[y\] is equal to zero. If we want to find \[y\] -intercept, then we have to set \[x\] is equal to
zero.
Set \[y = 0\]in the equation\[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = - 4{x^2} + 20x - 24\]
\[0 = - 4{x^2} + 20x - 24\]
Divide\[ - 4\]into both sides
\[0 = {x^2} - 5x + 24\]
By factoring the above equation we get,

So, we get
\[\left( {x - 2} \right)\left( {x - 3} \right) = 0\]
So, we get\[x = 3,x = 2\]when\[y = 0\]
Next set\[x = 0\]in the equation\[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = - 4{x^2} + 20x - 24\]
\[
y = - 4{\left( 0 \right)^2} + (20 \times 0) - 24 \\
y = 0 + 0 - 24 \\
\]
\[y = - 24\]
So, we get\[y = - 24\]when\[x = 0\]
So, we have,
\[y\]-intercept\[ = \left( {0, - 24} \right)\]
\[x\]-intercept\[ = \left( {3,0} \right),\left( {2,0} \right)\]
Vertex\[ = \left( {\dfrac{5}{2},1} \right)or\left( {2.5,1} \right)\]
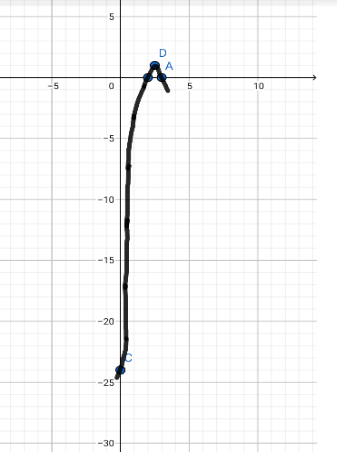
Let’s plot these points in the graph sheet as shown below,

Note: Remember the formula and conditions for x -intercept, y -intercept, and vertex point. Note that if a is negative the parabola shape will be in a downward position and if a is positive the parabola shape will be in an upward position. Also, this question describes the operation of addition/ subtraction/ multiplication/ division.