Question

Find the volume by counting the number of squares, if the side of each square is of length 1cm.

A) $$30\text{ c}{\text{m}}^3$$
B) $$31\text{ c}{\text{m}}^3$$
C) $$\text{28 c}{\text{m}}^3$$
D) $$\text{27 c}{\text{m}}^3$$

Answer 1

Hint:
To solve this question, we will count the number of squares forming each side of the figure. We will calculate the length, breadth, and height using the length and number of squares. We will then find the volume using the formula for volume of a cuboid.
Formula Used: We will use the formula of $$\text{Volume of cuboid = }l\times b\times h$$, where $$l$$ is the length of the cuboid, $$b$$ is the breadth of the cuboid, and$$h$$is the height of the cuboid.

Complete step by step solution:
To solve this question, let us first mark all of our faces. So, we get our figure as,

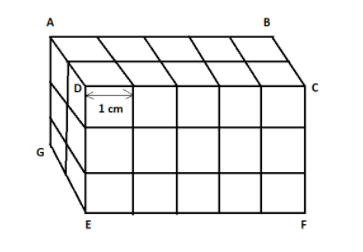
We will consider the face $$ABCD$$.
Now we can see that the side $$AB$$ of the rectangle $$ABCD$$ has 5 squares lined up forming it.
Hence, the side $$AB$$ is given as,
$$AB=5\times \text{ Side of 1 square}$$
On substituting the value of the side of 1 square in the above equation, we get,
$$AB=5\times 1=5\text{ cm}$$
We will now consider the face $$ADEG$$.
Now we can see that the side $$AD$$ of the rectangle $$ADEG$$ has 2 squares lined up forming it.
Hence, the side $$AD$$ is given as,
$$AD=2\times \text{ Side of 1 square}$$
On substituting the value of the side of 1 square in the above equation, we get,
$$AD=2\times 1=2\text{ cm}$$
We will consider the face $$CDEF$$.
Now we can see that the side $$DE$$ of the rectangle $$CDEF$$ has 3 squares lined up forming it.
Hence, the side $$DE$$ is given as,
$$DE=3\times \text{ Side of 1 square}$$
On substituting the value of the side of 1 square in the above equation, we get,
$$DE=3\times 1=3\text{ cm}$$
Therefore, we have obtained the sides of our cuboid as 5 cm, 2cm, and 3cm respectively.
So, now we will find the volume of the cuboid or our figure.
$$\text{Volume of cuboid = }l\times b\times h$$
Length of cuboid, $$l=AB=5\text{cm}$$
The breadth of cuboid, $$b=AD=2\text{cm}$$
Height of cuboid, $$h=DE=3\text{cm}$$
On substituting the above values in the formula for the volume of the cuboid, we get,
$$\text{Volume of cuboid = 5}\times 2\times 3\text{ = 30 c}{\text{m}}^3$$
Thus, the volume of our figure is $$\text{30 c}{\text{m}}^3$$.

So, the correct answer is option (A).

Note:
The alternate method to solve this question can be as follows –
We know that all the squares will be forming the three-dimensional cubes.
So, can calculate the volume of 1 cube and then multiply it with the total number of cubes.
We know that the volume of a cube is given as,
$$\text{Volume of cube}=a^3$$
Where $$a$$ is the side of the cube.
Here, we are given a side as 1 cm.
Hence, substituting this value in the formula for the volume of a cube, we get,
$$\text{Volume of cube}=1^3=1\text{ c}{\text{m}}^3$$
Thus, the value of the volume of 1 cube is $$\text{1 c}{\text{m}}^3$$.
We will now count the total number of cubes.
From the figure, we can see that there are 15 cubes stacked on the face $$CDEF$$. Also, the cubes are stacked in the rows of two. This is evident from the face $$ABCD$$.
So, the total number of cubes are,
$$\text{Total number of cubes}=15\times 2=30$$
Now we will find the Total volume of the 30 cubes. We know that the volume of 1 cube is $$\text{1 c}{\text{m}}^3$$.
$$\text{Total volume of all cubes}=30\times 1=30\text{ c}{\text{m}}^3$$
Thus, the volume of our figure is $$\text{30 c}{\text{m}}^3$$.