Question

Find the volume of a box if its length, breadth and height are 20 cm, 10.5 cm and 8 cm respectively.

Answer 1

Hint: We have given the length, breadth and height of the box as 20 cm, 10.5 cm and 8 cm. If you look carefully then you will find that all the length, breadth and height are unequal so the box is constructing a cuboid. We know that the volume of the cuboid is equal to the multiplication of length, breadth and height. The formula for volume of cuboid is equal to $l\times b\times h$ where “l, b and h” are length, breadth and height of the cuboid respectively.

Complete step-by-step answer:
We have given a box whose length, breadth and height is 20 cm, 10.5 cm and 8 cm.
As you can see, the length, breadth and height of the box are unequal so we can say that the box is in the form of a cuboid.
In the below figure, we have drawn a cuboid with length as “l”, breadth as “b” and height as “h”.

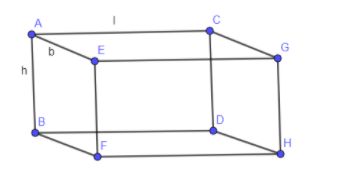
In the above diagram, we have represented length by AC, breadth by AE and height by AB.
We know that, the formula for volume of cuboid is equal to multiplication of length, breadth and height so writing the volume in mathematical form we get,
 Volume of cuboid is equal to:
$l\times b\times h$
Substituting “l” as 20 cm, “b” as 10.5 cm and “h” as 8 cm in the above expression we get,
$\begin{align}
  & \left( 20 \right)\times \left( 10.5 \right)\times \left( 8 \right) \\
 & =2\left( 105 \right)\left( 8 \right) \\
 & =1680c{{m}^{3}} \\
\end{align}$
Hence, the volume of the box is equal to $1680c{{m}^{3}}$.

Note:In the below, we are showing the proof for the volume of the cuboid.
The below picture is of a cuboid.

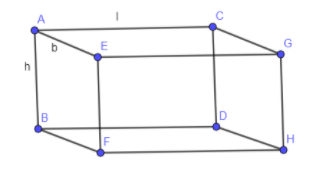
We know that the volume of any figure is the multiplication of the area of base with the height so the volume of the cuboid is calculated by multiplying the area of the base with the height h.
Area of base BDHF is equal to multiplication of length and breadth so area of base is equal to:
$l\times b$
Now, multiplying the above area of base by h we get the volume of cuboid.
$l\times b\times h$
Hence, we have shown the volume of the cuboid as $l\times b\times h$.