Question

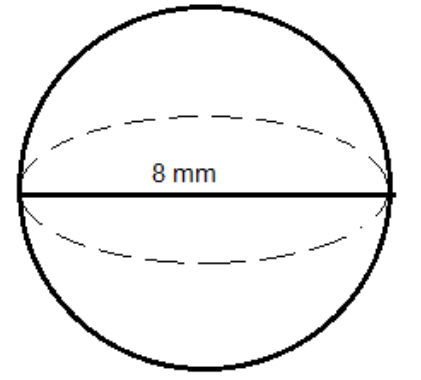
Find the volume of the sphere whose diameter is 8mm. (Take\[\pi = 3.14\]) (Round your answer to the nearest tenth)

Answer 1

Hint: A set of points in the space at a distance \[r\] from a fixed point (center) is known as the sphere. It is a perfectly round object in 3-dimensional space with no edges or vertices and is a perfectly symmetrical object. It is drawn on the three-axis x-axis, y-axis, and z-axis.
The volume of a shape is generally referred to as the capacity it has, or it can hold. The volume of the sphere determines the capacity of the gaseous state that can behold in it. The volume of the sphere is directly dependent on its diameter \[V \propto d\]; the larger the diameter of the sphere, the greater is its capacity, and the smaller the diameter of the sphere, the lesser capacity it has.

Complete step by step answer:
The volume of a Sphere is given as \[V = \dfrac{4}{3}\pi {r^3}\], where \[r\] is the radius of the sphere. Radius is the total distance of the center of the sphere to its boundary. Radius is represented as \[r = \dfrac{d}{2}\], where \[d\] is the diameter of the sphere.
The diameter of the sphere is given as \[d = 8{\text{ }}mm\] hence the radius will be:
\[
  r = \dfrac{d}{2} \\
   = \dfrac{8}{2} = 4mm \\
 \].
So the volume of the sphere will be:
\[
  V = \dfrac{4}{3}\pi {r^3} \\
   = \dfrac{4}{3}\pi {\left( 4 \right)^3} \\
   = \dfrac{4}{3} \times 3.14 \times 4 \times 4 \times 4 \\
   = \dfrac{{256 \times 3.14}}{3} \\
   = 267.95{\left( {mm} \right)^3} \\
 \]

Hence, the volume of the sphere is 267.95 cubic milli-meters.

Note: To find the capacity of a closed curve/body, the volume is calculated for a three-dimensional object, and the area is calculated for a two-dimensional figure. The three-dimensional sphere is obtained when a two-dimensional circle is rotated about its symmetry.