Question

Find the x-intercept and y-intercept of the circle $ {{x}^{2}}+{{y}^{2}}-8x+y-20=0 $ . Hence find the length of the chord cut by the circle on the x-axis and y-axis.

Answer 1

Hint: We should know that an x-intercept is where the graph touches or crosses the x-axis and a y-intercept is where the graph touches or crosses the y-axis. To find the x-intercept, we will assume that $ y=0 $ and then solve for x. Similarly, we will assume $ x=0 $ and solve for y to get the y-intercept. We should also remember that the equation of a circle at the centre (a, b) and a radius r is given by $ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} $ . We will use these concepts and get the required answer.

Complete step-by-step answer:
In the question here, we are given the equation of the circle as,
  $ {{x}^{2}}+{{y}^{2}}-8x+y-20=0\ldots \ldots \ldots \left( i \right) $
We are asked to find the x intercept as well as the y intercept, that is the points where the circle crosses the x-axis and the y-axis. So, we will first find the point where the circle crosses the x-axis. For that we will assume $ y=0 $ and solve the equation (i). So, putting $ y=0 $ in equation (i), we get,
 $ {{x}^{2}}-8x-20=0 $
Now, we will use the splitting the middle term method to solve for x. Here we have $ -10+2=-8 $ and $ -10\times 2=-20 $ . So, we will substitute these in the above equation. So, we get,
 $ {{x}^{2}}-10x+2x-20=0 $
We will rearrange the terms to get,
 $ x\left( x-10 \right)+2\left( x-10 \right)=0 $
And this can be written as follows,
 $ \begin{align}
  & \left( x-10 \right)\left( x+2 \right)=0 \\
 & \Rightarrow x=10,-2 \\
\end{align} $
Therefore, we get that the circle $ {{x}^{2}}+{{y}^{2}}-8x+y-20=0 $ cuts the x axis at the following points of (10, 0) and (-2, 0). Now let us find the y intercept. Now, in this case, we will assume $ x=0 $ and solve for y. So, putting the value of $ x=0 $ in equation (i), we get,
 $ {{y}^{2}}+y-20=0 $
We will again split the middle term to solve for y. Here we have $ +5-4=1 $ and $ +5\times -4=-20 $ . So, we get,
 $ \begin{align}
  & {{y}^{2}}+5y-4y-20=0 \\
 & \Rightarrow y\left( y+5 \right)-4\left( y+5 \right)=0 \\
\end{align} $
We can rewrite this as follows,
 $ \begin{align}
  & \left( y+5 \right)\left( y-4 \right)=0 \\
 & \Rightarrow y=4,-5 \\
\end{align} $
Thus, we get that the circle $ {{x}^{2}}+{{y}^{2}}-8x+y-20=0 $ cuts the x axis at the points (0, 4) and (0, -5). The given equation of the circle can be written in the standard form as follows,
\[\begin{align}
  & {{x}^{2}}+\left( -8x \right)+{{4}^{2}}-{{4}^{2}}+{{y}^{2}}+y+{{\left( \dfrac{1}{2} \right)}^{2}}-{{\left( \dfrac{1}{2} \right)}^{2}}=20 \\
 & \Rightarrow {{x}^{2}}+\left( -8x \right)+{{4}^{2}}+{{y}^{2}}+y+{{\left( \dfrac{1}{2} \right)}^{2}}-16-\dfrac{1}{4}=20 \\
 & \because {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}} \\
 & \Rightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-\left( -\dfrac{1}{2} \right) \right)}^{2}}=16+\dfrac{1}{4}+20 \\
 & \Rightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-\left( -\dfrac{1}{2} \right) \right)}^{2}}=\dfrac{145}{4} \\
 & \Rightarrow {{\left( x-4 \right)}^{2}}+{{\left( y-\left( -\dfrac{1}{2} \right) \right)}^{2}}={{\left( \dfrac{\sqrt{145}}{4} \right)}^{2}} \\
\end{align}\]
Now, we have the general form as $ {{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}} $ , we know that (a,b) is the center and r is the radius.
So, comparing we get that this is a circle with the centre at $ \left( 4,-\dfrac{1}{2} \right) $ and radius $ \dfrac{\sqrt{145}}{4}=6.02units $ . We will now plot this on the graph as below.

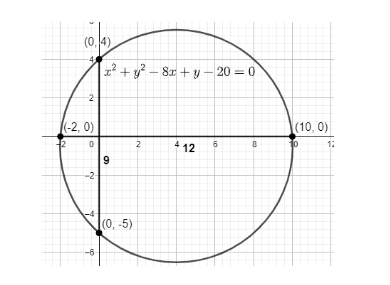
We will use the coordinates to find the length of the chord, since we have the x or the y coordinate as 0 in this case.
So, we have points as (10,0) and (-2,0). Therefore, we can see from the above graph that the length of the chord cut by the circle on the x-axis = 10 – (-2) = 10 + 2 = 12 units.
Also, we have points (0,4) and (0,-5). So, we can also see that the length of the chord cut by circle on the y-axis = 4 – (-5) = 4 + 5 = 9 units.

Note: We should always remember while plotting the graph that we have to set the scale of the graph, if there are any measurements that have to be plotted on the graph, then we should change it accordingly with the scale that you have chosen. We should also remember that we can have the radius, $ r=\sqrt{{{g}^{2}}+{{f}^{2}}-c} $ from the circle equation that is given in the form of $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ . We can also use the distance formula to find the length of the chords since we have the coordinates of both the intercepts on both the axes. So, for x-axis, we will have it as
 $ \begin{align}
  & d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} \\
 & d=\sqrt{{{\left( -2-10 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}} \\
 & d=\sqrt{{{\left( -12 \right)}^{2}}} \\
 & d=\sqrt{144} \\
 & d=12units \\
\end{align} $
Similarly, we can compute for y-axis too.