Question

How do you find trigonometric ratios of 30, 45, and 60 degrees?

Answer 1

Hint: Right-angled triangle in an equilateral triangle (which is formed by dropping altitude from any vertex to its opposite side) and isosceles right-angled triangle are considered to be special right triangles. From these triangles, we can find the trigonometric ratios of basic angles. Trigonometric ratios are the ratios of the sides of some standard triangles like a special right triangle. In a triangle, according to the Pythagorean theorem, the sum of squares of the length of two adjacent sides is equal to the square of the length of the opposite side.

Complete step-by-step solution:
As per the given question, we have trigonometric ratios of 30, 45, and 60 degrees. Both \[30{}^\circ \] and \[60{}^\circ \] are based on an equilateral triangle with sides of length 2 and one of the angles bisected.
The \[45{}^\circ \] angle is based on an isosceles triangle with the equal sides having a length of 1.
Now, let’s consider the equilateral triangle which is shown below:

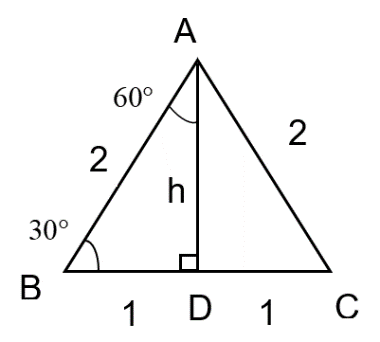
Using Pythagorean theorem, \[{{2}^{2}}={{1}^{2}}+{{h}^{2}}\Rightarrow h=\sqrt{{{2}^{2}}-{{1}^{2}}}\Rightarrow h=\sqrt{3}\]. We know that,
\[\begin{align}
  & \sin =\dfrac{opposite(side)}{hypotenuse} \\
 & \cos =\dfrac{adjacent(side)}{hypotenuse} \\
 & \tan =\dfrac{opposite(side)}{adjacent(side)} \\
 & \sec =\dfrac{1}{\cos } \\
 & \cot =\dfrac{1}{\tan } \\
\end{align}\]
cosec \[=\dfrac{1}{\sin }\]
Therefore, the trigonometric ratios of \[30{}^\circ \] and \[60{}^\circ \]are
\[\begin{align}
  & \Rightarrow \sin (30{}^\circ )=\dfrac{1}{2},\sin (60{}^\circ )=\dfrac{\sqrt{3}}{2} \\
 & \Rightarrow \cos (30{}^\circ )=\dfrac{\sqrt{3}}{2},\cos (30{}^\circ )=\dfrac{1}{2} \\
 & \Rightarrow \tan (30{}^\circ )=\dfrac{1}{\sqrt{3}},\tan (60{}^\circ )=\dfrac{\sqrt{3}}{1}=\sqrt{3} \\
 & \Rightarrow \sec (30{}^\circ )=\dfrac{1}{\cos (30{}^\circ )}=\dfrac{1}{\dfrac{\sqrt{3}}{2}}=\dfrac{2}{\sqrt{3}},\sec (60{}^\circ )=\dfrac{1}{\cos (60{}^\circ )}=\dfrac{1}{\dfrac{1}{2}}=2 \\
 & \Rightarrow \cot (30{}^\circ )=\dfrac{1}{\tan 30{}^\circ }=\dfrac{1}{\dfrac{1}{\sqrt{3}}}=\sqrt{3},\cot (60{}^\circ )=\dfrac{1}{\tan (60{}^\circ )}=\dfrac{1}{\sqrt{3}} \\
 & \\
\end{align}\]
\[\Rightarrow \]cosec (\[30{}^\circ \])\[=\dfrac{1}{\sin (30{}^\circ )}=\dfrac{1}{\dfrac{1}{2}}=2,\]
\[\Rightarrow \]cosec (\[60{}^\circ \])\[=\dfrac{1}{\sin (60{}^\circ )}=\dfrac{1}{\dfrac{\sqrt{3}}{2}}=\dfrac{2}{\sqrt{3}}\].
Now, let’s consider the isosceles right triangle to find trigonometric ratios of \[45{}^\circ \]as shown below:

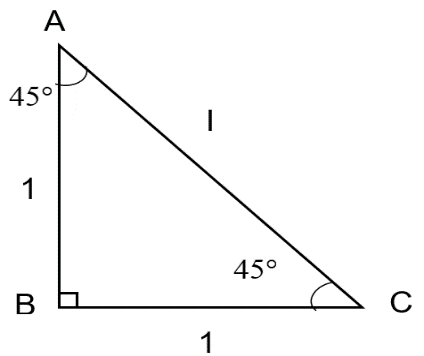
Using Pythagorean theorem, length \[l=\sqrt{{{1}^{2}}+{{1}^{2}}}=\sqrt{2}\].
Therefore, the trigonometric ratios of \[45{}^\circ \]are
\[\begin{align}
  & \Rightarrow \sin (45{}^\circ )=\dfrac{1}{\sqrt{2}} \\
 & \Rightarrow \cos (45{}^\circ )=\dfrac{1}{\sqrt{2}} \\
 & \Rightarrow \tan (45{}^\circ )=\dfrac{1}{1}=1 \\
 & \Rightarrow \sec (45{}^\circ )=\dfrac{1}{\cos (45{}^\circ )}=\dfrac{1}{\dfrac{1}{\sqrt{2}}}=\sqrt{2} \\
 & \Rightarrow \cot (45{}^\circ )=\dfrac{1}{\tan (45{}^\circ )}=\dfrac{1}{1}=1 \\
\end{align}\]
\[\Rightarrow \]cosec (\[45{}^\circ \])\[=\dfrac{1}{\sin (45{}^\circ )}=\dfrac{1}{\dfrac{1}{\sqrt{2}}}=\sqrt{2}\].

Note: While finding the trigonometric ratios of a triangle, if we have sine, cosine, and tangent values, then we can calculate the cosecant, secant, and cotangent of the triangle. And we know that for \[sin(n\times 90{}^\circ -\theta )\], it is equal to \[\pm \]\[\sin \theta \] if n is even and it is equal to \[\pm \cos \theta \] as cosine is the complement of sine function. So, if we have a sine value of 30 degrees then we find a cosine value of 60 degrees.