
What is the flux over a curved surface of the hemisphere?

Answer
513.3k+ views
Hint:The rate of flow of electric field lines through a given area is known as electric flux $\left( {{\phi _E}} \right)$ .$S.I$ Unit for electric flux is $\left( {\dfrac{{N{m^2}}}{C}} \right)$ . Area vector$\overrightarrow {(A)} $ is a vector whose magnitude is equal to the area and direction is perpendicular and away from the surface.
Complete step by step answer:
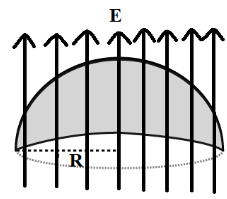
The electric flux over a curved surface area of the hemisphere can be represented as shown in the figure below, let $R$be the radius of the hemisphere.
The electric flux$\left( {{\phi _E}} \right)$ is given by the equation,
${\phi _E} = EA\cos \theta $.
Where $\theta $ is the angle between electric field $\left( E \right)$ and area vector $\left( A \right)$.
${\phi _E} = EA\cos 180$.
The angle between the electric field $\left( E \right)$ and the area vector $\left( A \right)$is ${180^0}$.
${\phi _E} = - EA$.......................$\left( {\because \cos 180 = - 1} \right)$
We know that, the area of circle is $\pi {r^2}$,
$\therefore {\phi _E} = - E\pi {R^2}$
Hence, the flux over a curved surface of the hemisphere is $- E\pi {R^2}$.
Note: We need to consider the area of the circle not the area of the hemisphere because the electric field lines pass through the base of the hemisphere and the base of the hemisphere is a circle. Negative sign indicates that the direction of electric field lines and area vectors is opposite.
Complete step by step answer:
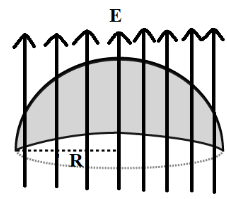
The electric flux over a curved surface area of the hemisphere can be represented as shown in the figure below, let $R$be the radius of the hemisphere.

The electric flux$\left( {{\phi _E}} \right)$ is given by the equation,
${\phi _E} = EA\cos \theta $.
Where $\theta $ is the angle between electric field $\left( E \right)$ and area vector $\left( A \right)$.
${\phi _E} = EA\cos 180$.
The angle between the electric field $\left( E \right)$ and the area vector $\left( A \right)$is ${180^0}$.
${\phi _E} = - EA$.......................$\left( {\because \cos 180 = - 1} \right)$
We know that, the area of circle is $\pi {r^2}$,
$\therefore {\phi _E} = - E\pi {R^2}$
Hence, the flux over a curved surface of the hemisphere is $- E\pi {R^2}$.
Note: We need to consider the area of the circle not the area of the hemisphere because the electric field lines pass through the base of the hemisphere and the base of the hemisphere is a circle. Negative sign indicates that the direction of electric field lines and area vectors is opposite.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

The computer jargonwwww stands for Aworld wide web class 12 physics CBSE

State the principle of an ac generator and explain class 12 physics CBSE




