
What is the focal length of a double convex lens for which the radius of curvature of each surface is 60 cm (n=1.5)?
A. 50 cm
B. 60 cm
C. 90 cm
D. 30 cm
Answer
499.5k+ views
Hint: Generally, if nothing is given about the lens, we take it to be thin and having focal length independent of the refractive index. In that case, we take focal length as half of the radius of curvature. But practically, the lens has thickness and the parameters depend upon the refractive index also.
Formula used:
Complete step by step answer:
For computing the focal length of any lens, we practically use the formula called lens makers formula. This formula is given by
Here,
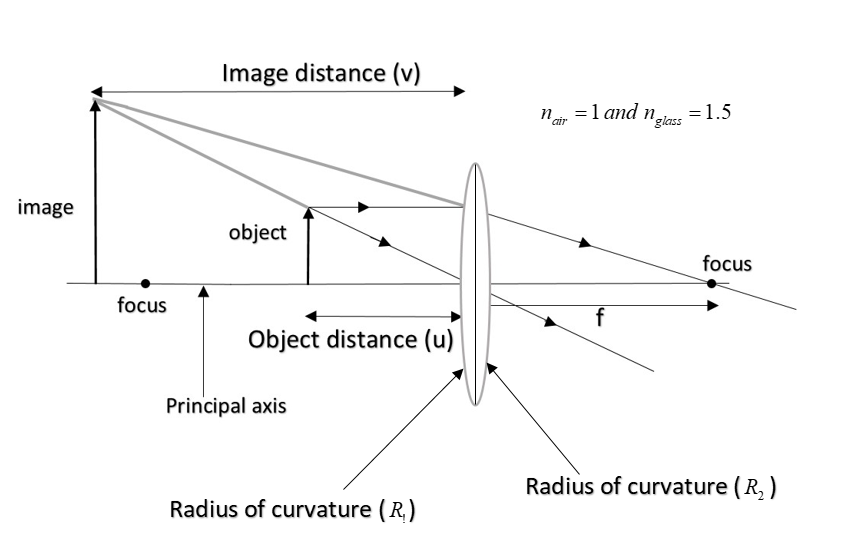
Given,
Also given that the radii of curvature for both sides is the same. But, for the left side, we will take radius to be positive whereas for the right side, we will take radius to be negative (as per the sign conventions).
Hence
Putting the values in the equation:
Or
Hence, the focal length of the double convex lens is -60 cm.
Note:
Students should note that in case of a thin lens, we directly take ‘f’ as half of ‘R’. But in this question, we have the value of ‘R’ and ‘f’ is the same. One must not confuse between a thin and practical lens. Whenever the refractive index of the material is given and the lens is not thin, we have to calculate the focal length of the lens using the lens makers formula.
Formula used:
Complete step by step answer:
For computing the focal length of any lens, we practically use the formula called lens makers formula. This formula is given by
Here,

Given,
Also given that the radii of curvature for both sides is the same. But, for the left side, we will take radius to be positive whereas for the right side, we will take radius to be negative (as per the sign conventions).
Hence
Putting the values in the equation:
Or
Hence, the focal length of the double convex lens is -60 cm.
Note:
Students should note that in case of a thin lens, we directly take ‘f’ as half of ‘R’. But in this question, we have the value of ‘R’ and ‘f’ is the same. One must not confuse between a thin and practical lens. Whenever the refractive index of the material is given and the lens is not thin, we have to calculate the focal length of the lens using the lens makers formula.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




