
For a regular hexagon with apothem 5 m, the side length is about 5.77 m. The area of the regular hexagon is \[\left( \text{in }{{m}^{2}} \right).\]
(a) 75.5
(b) 85.5
(c) 76.5
(d) 86.5
Answer
125.7k+ views
Hint: To solve the given question, we will first find out what a regular hexagon is and what an apothem in a regular hexagon is. Then we will draw a rough sketch of the hexagon and we will make an apothem in it. Then, we will join the center of the hexagon with the two consecutive vertexes of the hexagon. After doing this, we will find the area of the triangle formed by the construction. Then we will multiply this area by 6 to get the total area of the regular hexagon.
Complete step-by-step answer:
Before solving the question, we must know what a regular hexagon is and what an apothem is. A hexagon is a polygon that has 6 sides and 6 interior angles. An apothem of a hexagon is a line segment from the center of a hexagon to the middle point of any one side of the hexagon. A rough sketch of a hexagon with an apothem is shown.
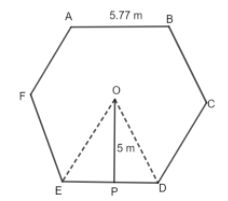
In the above figure, OP is the apothem. Now, we will find the area of triangle ODE. The area of any triangle with the base b and height h is given by the formula shown below.
\[\text{Area}=\dfrac{1}{2}\times b\times h\]
In our case, b = DE and h = OP. Thus, we have,
\[\text{Area}=\dfrac{1}{2}\times DE\times OP\]
\[\Rightarrow \text{Area of DE}=\dfrac{1}{2}\times 5.77m\times 5m\]
\[\Rightarrow \text{Area of }\Delta \text{ODE}=14.425{{m}^{2}}\]
Now, there will be a total of 6 similar triangles, so the area of the hexagon will be six times the area of triangle ODE. Thus, we have,
\[\text{Area of hexagon}=6\times \text{Area of }\Delta \text{ODE}\]
\[\Rightarrow \text{Area of hexagon}=6\times 14.425{{m}^{2}}\]
\[\Rightarrow \text{Area of hexagon}=86.55{{m}^{2}}=86.5{{m}^{2}}\]
Hence, option (d) is the right answer.
Note: An alternate way of solving the above question is shown below. The area of the hexagon with side ‘s’ is given by the formula shown.
\[\text{Area of hexagon}=\dfrac{3\sqrt{3}}{2}{{s}^{2}}\]
where s = 5.77 m in our case. Thus, we will get,
\[\text{Area of hexagon}=\dfrac{3\sqrt{3}}{2}{{\left( 5.77m \right)}^{2}}\]
\[\Rightarrow \text{Area of hexagon}=\dfrac{3\times 1.732}{2}\times 33.2929{{m}^{2}}\]
\[\Rightarrow \text{Area of hexagon}=86.4949{{m}^{2}}\simeq 86.5{{m}^{2}}\]
Complete step-by-step answer:
Before solving the question, we must know what a regular hexagon is and what an apothem is. A hexagon is a polygon that has 6 sides and 6 interior angles. An apothem of a hexagon is a line segment from the center of a hexagon to the middle point of any one side of the hexagon. A rough sketch of a hexagon with an apothem is shown.

In the above figure, OP is the apothem. Now, we will find the area of triangle ODE. The area of any triangle with the base b and height h is given by the formula shown below.
\[\text{Area}=\dfrac{1}{2}\times b\times h\]
In our case, b = DE and h = OP. Thus, we have,
\[\text{Area}=\dfrac{1}{2}\times DE\times OP\]
\[\Rightarrow \text{Area of DE}=\dfrac{1}{2}\times 5.77m\times 5m\]
\[\Rightarrow \text{Area of }\Delta \text{ODE}=14.425{{m}^{2}}\]
Now, there will be a total of 6 similar triangles, so the area of the hexagon will be six times the area of triangle ODE. Thus, we have,
\[\text{Area of hexagon}=6\times \text{Area of }\Delta \text{ODE}\]
\[\Rightarrow \text{Area of hexagon}=6\times 14.425{{m}^{2}}\]
\[\Rightarrow \text{Area of hexagon}=86.55{{m}^{2}}=86.5{{m}^{2}}\]
Hence, option (d) is the right answer.
Note: An alternate way of solving the above question is shown below. The area of the hexagon with side ‘s’ is given by the formula shown.
\[\text{Area of hexagon}=\dfrac{3\sqrt{3}}{2}{{s}^{2}}\]
where s = 5.77 m in our case. Thus, we will get,
\[\text{Area of hexagon}=\dfrac{3\sqrt{3}}{2}{{\left( 5.77m \right)}^{2}}\]
\[\Rightarrow \text{Area of hexagon}=\dfrac{3\times 1.732}{2}\times 33.2929{{m}^{2}}\]
\[\Rightarrow \text{Area of hexagon}=86.4949{{m}^{2}}\simeq 86.5{{m}^{2}}\]
Recently Updated Pages
Difference Between Area and Volume

Difference Between Mutually Exclusive and Independent Events

JEE Main 2025 Sample Question Paper-1 with Answer Keys - Free PDF

JEE Main Previous Year Question Paper with Answers - Download FREE PDF

JEE Main Sample Papers 2025 with Solutions - FREE PDF Download

JEE Main 2025 22 Jan Shift 1 Physics Answer Key with Solutions

Trending doubts
JEE Main Marks Vs Percentile Vs Rank 2025: Calculate Percentile Using Marks

JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Cutoff 2025 – Official Cutoff Release Date | Expected Cutoff Marks

JEE Main Marks vs Rank 2025

JEE Main 2025 22 Jan Shift 1 Question Paper with Solutions

NIT Cutoff Percentile for 2025

Other Pages
NCERT Solutions for Class 9 Maths Chapter 9 Circles

NCERT Solutions for Class 9 Maths Chapter 11 Surface Area and Volume

NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas And Volumes Ex 11.3

NCERT Solutions for Class 9 Maths Chapter 12 Statistics

NCERT Solutions for Class 9 Maths Chapter 10 Heron'S Formula

NCERT Solutions for Class 9 Maths In Hindi Chapter 1 Number System




