Question

For a simple pendulum, relation between time period $T$, length of pendulum $l$ and acceleration due to gravity $g$is given by:
A. $T = 2\pi \dfrac{l}{{\sqrt g }}$
B. $T = 2\pi \sqrt {\dfrac{l}{g}} $
C. $T = 2\pi \dfrac{l}{g}$

Answer 1

Hint: The time period of the simple pendulum is defined as the time required to complete one complete cycle of oscillation.
Restoring force ${f_e}$ for the simple pendulum is:
${f_e} = - mg\sin \theta $
Here, $m$mass of the suspended particle, $g$acceleration due to gravity and $\theta $ is angular displacement from the me
a position.
For simple harmonic oscillation acceleration $a$ is given as,
$a = - {\omega ^2}x$
Here, $\omega $ is frequency of oscillation and x is the distance of mass from the attachment of the string.

Complete step by step answer:
It is given that the time period of oscillation is $T$, the length of the pendulum $l$ and the acceleration due to gravity $g$.
You have to find the relation between these quantities.
First we will calculate the time period of the simple pendulum using the formula given below,
$T = \dfrac{{2\pi }}{\omega }$ ….. (1)
You have to determine this $\omega $.

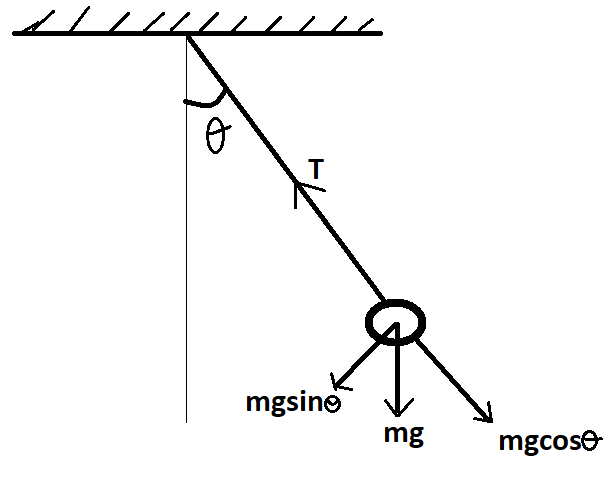
Figure: simple pendulum.
Consider a simple pendulum (figure above) a small angular displacement $\theta $. The $\cos \theta $ component of $mg$is balanced by the tension of the string. And the $\sin \theta $ component of the $mg$ work as restoring force so,
${f_e} = - mg\sin \theta $.
Here, $\theta $ is very less so $\sin \theta \approx \theta $
$\theta $ for this pendulum is given as $\theta = \dfrac{x}{l}$, $x$ is distance of mass from the string is attached.
Using the above equation,
${f_e} = - mg(\dfrac{x}{l})$
The acceleration is given as $a = \dfrac{{{f_e}}}{m}$,
$a = - g\left( {\dfrac{x}{l}} \right)$ …… (2)
For simple harmonic oscillation acceleration $a$ is given as,
$a = - {\omega ^2}x$ …... (3)
Compare equation 1 and 2,
$ - g\left( {\dfrac{x}{l}} \right) = - {\omega ^2}x$
Now, solve for $\omega $,
$\omega = \sqrt {\dfrac{g}{l}} $ …… (4)
Put value of $\omega $ from equation 4 to equation 1,
$T = 2\pi \sqrt {\dfrac{l}{g}} $.

So, the correct answer is “Option B”.

Note:
Always choose a coordinate system for such a problem and all measurements should be made from that coordinate system. First find the force acting on mass then make components of that force and equate the force to get the equation of motion.