
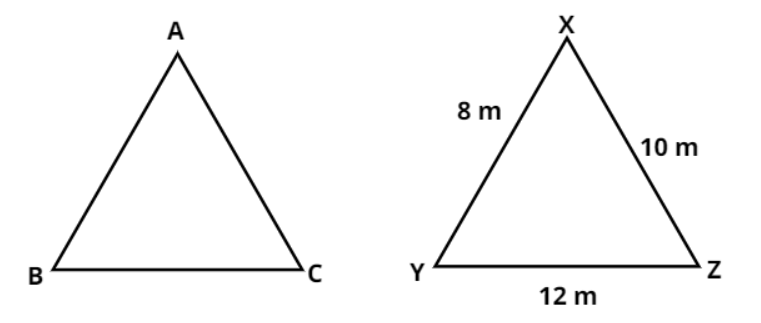
For a $\vartriangle {\text{XYZ}}$, ${\text{ZY}} = 12{\text{ m}}$, ${\text{YX}} = 8{\text{ m}}$ and ${\text{XZ}} = 10{\text{ m}}$. If $\vartriangle {\text{ZYX}} \cong \vartriangle {\text{ABC}}$, then the length of side AC (in meters) is
$
{\text{A}}{\text{. 10}} \\
{\text{B}}{\text{. 12}} \\
{\text{C}}{\text{. 8}} \\
{\text{D}}{\text{. 1}} \\
$
Answer
123k+ views
Hint- Here, we will be using the property that the length of the corresponding sides will be equal in any two congruent triangles.
Given, in a $\vartriangle {\text{XYZ}}$, ${\text{ZY}} = 12{\text{ m}}$, ${\text{YX}} = 8{\text{ m}}$ and ${\text{XZ}} = 10{\text{ m}}$
Since we know that for any two congruent triangles, the corresponding sides are always equal.
Also given that $\vartriangle {\text{ZYX}} \cong \vartriangle {\text{ABC}}$
Clearly from the figure, we can see that the side AB in $\vartriangle {\text{ABC}}$ is corresponding to side XY in $\vartriangle {\text{XYZ}}$, side BC in $\vartriangle {\text{ABC}}$ is corresponding to side YZ in $\vartriangle {\text{XYZ}}$ and side AC in $\vartriangle {\text{ABC}}$ is corresponding to side XZ in $\vartriangle {\text{XYZ}}$.
i.e., we can say ${\text{AB}} = {\text{XY}} = {\text{YX}} = 8{\text{ m}}$, ${\text{BC}} = {\text{YZ}} = {\text{ZY}} = 12{\text{ m}}$ and ${\text{AC}} = {\text{XZ}} = 10{\text{ m}}$.
Hence, the length of side AC is 10 meters.
Therefore, option A is correct.
Note- In these type of problems, the corresponding sides of the given congruent triangles are needed to be identified carefully with the help of their diagrams.
Given, in a $\vartriangle {\text{XYZ}}$, ${\text{ZY}} = 12{\text{ m}}$, ${\text{YX}} = 8{\text{ m}}$ and ${\text{XZ}} = 10{\text{ m}}$
Since we know that for any two congruent triangles, the corresponding sides are always equal.
Also given that $\vartriangle {\text{ZYX}} \cong \vartriangle {\text{ABC}}$
Clearly from the figure, we can see that the side AB in $\vartriangle {\text{ABC}}$ is corresponding to side XY in $\vartriangle {\text{XYZ}}$, side BC in $\vartriangle {\text{ABC}}$ is corresponding to side YZ in $\vartriangle {\text{XYZ}}$ and side AC in $\vartriangle {\text{ABC}}$ is corresponding to side XZ in $\vartriangle {\text{XYZ}}$.
i.e., we can say ${\text{AB}} = {\text{XY}} = {\text{YX}} = 8{\text{ m}}$, ${\text{BC}} = {\text{YZ}} = {\text{ZY}} = 12{\text{ m}}$ and ${\text{AC}} = {\text{XZ}} = 10{\text{ m}}$.
Hence, the length of side AC is 10 meters.
Therefore, option A is correct.
Note- In these type of problems, the corresponding sides of the given congruent triangles are needed to be identified carefully with the help of their diagrams.
Recently Updated Pages
Difference Between Mutually Exclusive and Independent Events

Difference Between Area and Volume

Area of a Rhombus Formula | Perimeter and Area of Rhombus

Difference Between Power and Exponent: JEE Main 2024

Algebraic Formula

Difference Between Constants and Variables: JEE Main 2024

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main 2025 22 Jan Shift 1 Question Paper with Solutions

JEE Main Physics Question Paper with Answer Keys and Solutions

JEE Main Question Papers 2025

JEE Main 27 January 2024 Shift 1 Question Paper with Solutions

JEE Main Sample Paper (Set 1) with Solutions (2024-25)

Other Pages
NCERT Solutions for Class 9 Maths Chapter 9 Circles

NCERT Solutions for Class 9 Maths Chapter 11 Surface Area and Volume

NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas And Volumes Ex 11.3

NCERT Solutions for Class 9 Maths Chapter 12 Statistics

NCERT Solutions for Class 9 Maths Chapter 10 Heron'S Formula

NCERT Solutions for Class 9 Maths In Hindi Chapter 1 Number System




