Question

For anisotropic solids, coefficient of volume expansion is most appropriately given as (where symbols have their usual meanings)
A. \[3{\alpha _x}\]
B. \[{\alpha _x} + {\alpha _y} + {\alpha _z}\]
C. \[2{\alpha _x} + 2{\alpha _y}\]
D. \[3{\alpha _z} + {\alpha _x} - {\alpha _y}\]

Answer 1

Hint: Find the coefficient of linear expansion for each sides and then use the formula to find the coefficient of volume expansion then compare them to get the relation between the coefficient of volume expansion to linear expansion.

Formula used:
The linear expansion of any solid is given by,
\[l' = {l_0}(1 + \alpha \Delta T)\]
where, \[l'\] is the expanded length of the solid during change in temperature \[\Delta T\] , \[{l_0}\] is the initial length and \[\alpha \] is the expansion coefficient.
The volume expansion of any solid,
\[V' = {V_0}(1 + \gamma \Delta T)\]
where, \[V'\]is the expanded volume of the solid during change in temperature \[\Delta T\] , \[{V_0}\] is the initial length and \[\gamma \] is the expansion coefficient.

Complete step by step answer:
We have here an anisotropic solid and we have to find the relation between the coefficient of volume expansion and the coefficient of linear expansion. Now, since anisotropic solids stretch in length in different directions.

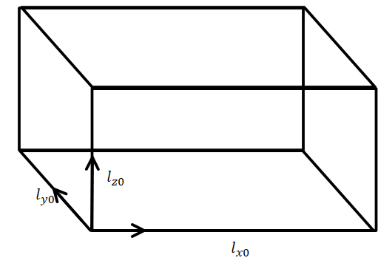
So, let the change in length along different axes are,
Change along the x axis: \[{l_x}' = {l_{x0}}(1 + {\alpha _x}\Delta T)\]
Change along the y axis: \[{l_y}' = {l_{y0}}(1 + {\alpha _y}\Delta T)\]
Change along the z axis: \[{l_z}' = {l_{z0}}(1 + {\alpha _z}\Delta T)\]

So, multiplying this three equations we will have,
\[{l_x}'{l_y}'{l_z}' = {l_{z0}}(1 + {\alpha _z}\Delta T){l_{y0}}(1 + {\alpha _y}\Delta T){l_{x0}}(1 + {\alpha _x}\Delta T)\]
Or, \[{l_x}'{l_y}'{l_z}' = {l_{z0}}{l_{y0}}{l_{x0}}(1 + {\alpha _z}\Delta T)(1 + {\alpha _y}\Delta T)(1 + {\alpha _x}\Delta T)\]
Now, neglecting the higher order terms of \[\alpha \] (since the dimension of \[\alpha \]is very small so, \[{\alpha ^2},{\alpha ^3} < < \alpha \])
We will have,
\[{l_x}'{l_y}'{l_z}' = {l_{z0}}{l_{y0}}{l_{x0}}[1 + ({\alpha _x} + {\alpha _y} + {\alpha _z})\Delta T]\]

Now, the \[{l_x}'{l_y}'{l_z}'\] is equal to the volume after the change and \[{l_{z0}}{l_{y0}}{l_{x0}}\] is the initial volume.
So, replacing them we will have,
\[V' = {V_0}[1 + ({\alpha _x} + {\alpha _y} + {\alpha _z})\Delta T]\]
Now, we know that the volume expansion of any solid,
\[V' = {V_0}(1 + \gamma \Delta T)\]
where, \[V'\] is the expanded volume of the solid during change in temperature \[\Delta T\] , \[{V_0}\] is the initial length and \[\gamma \] is the volume expansion coefficient.
So, comparing these two equations we can write,
\[\therefore \gamma = ({\alpha _x} + {\alpha _y} + {\alpha _z})\]
Hence, the coefficient of volume expansion of anisotropic solid to linear expansion of is given by \[({\alpha _x} + {\alpha _y} + {\alpha _z})\]

Hence, option B is the correct answer.

Note: The relation of coefficient of volume expansion and linear expansion for different types of solid is different. Here, we can see that for anisotropic solid it is different in different direction but for isotropic solid it is same in every direction for that we will have the relation as, \[\gamma = 3{\alpha _x} = 3{\alpha _y} = 3{\alpha _z}\].