Question

For drawing the perpendicular bisector of $PQ$, which of the following radii can be taken to draw arcs from $P$ and $Q$?
A. $\dfrac{{PQ}}{2}$
B. $\dfrac{{PQ}}{3}$
C. $\dfrac{{2PQ}}{3}$
D. $\dfrac{{PQ}}{4}$

Answer 1

Hint:To draw the perpendicular bisector on a given line segment, we have to keep the compass apart greater than half the distance between end points of the line segment. Then we draw arcs from both the end points to get the intersection points on each side of the line segment. At last, we join these intersection points to make the required perpendicular bisector. The underlined part is the main key to solve this problem.

Complete step-by-step answer:
Let us recall steps of construction of a perpendicular bisector DE on a line segment PQ .

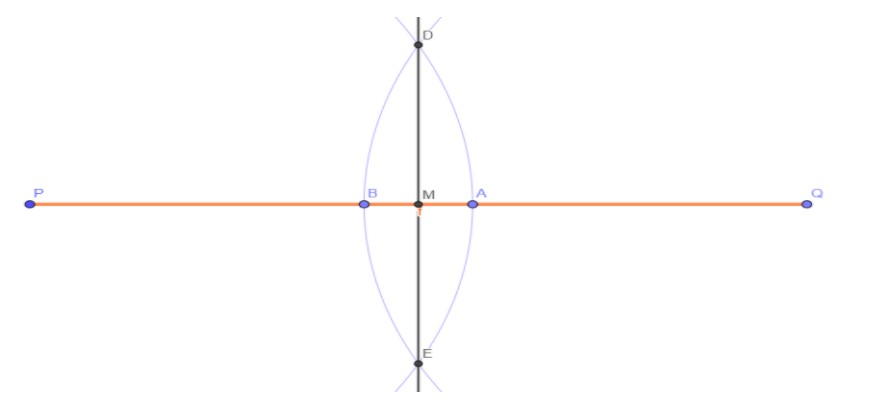
Figure 1 Construction of perpendicular bisector
Steps of Construction:
1.Let’s draw a line segment $PQ$.
2.Keep the compass apart greater than half of $PQ$ and scribe arcs from $P$ and $Q$ keeping the radii the same.
3.Name the points of intersection of the two arcs as $D$ and $E$. Join $DE$.
4.Thus, $DE$ is the perpendicular bisector on $PQ$. Name the point where $DE$ intersects $PQ$ as $M$ (obviously, it is the midpoint of line segment $PQ$).
From these steps, it is obvious that the radii of the arcs must be greater than half of the distance between the endpoints.
The distance between the end points of the line segment $PQ$ is the length of the line segment.
Length of the line segment $PQ$ is denoted by $PQ$. Thus, we can conclude that the radii of the arcs must be the same and greater than half of the length of the line segment.
Mathematically,
$radius > \dfrac{{PQ}}{2}$ ………………… Eq. I
Also from Figure 1, we may conclude the following
$radius = PA = QB$ …………… Eq. II
Let’s try to ponder over the four options as given in the problem:
A. $radius = \dfrac{{PQ}}{2}( = \dfrac{{PQ}}{2})$
B. $radius = \dfrac{{PQ}}{3}( < \dfrac{{PQ}}{2})$
C. $radius = \dfrac{{2PQ}}{3}( > \dfrac{{PQ}}{2})$
D. $radius = \dfrac{{PQ}}{4}( < \dfrac{{PQ}}{2})$

Hence, by the principle stated in Eq. I, we see that option (C) is correct.

So, the correct answer is “Option C”.

Note:Let’s solve the problem geometrically by drawing a line segment $PQ = 12cm$(suppose) and then taking arcs from end points $P,Q$ of radii as given in the four options. In doing so, we can practically examine the possibility of construction of a perpendicular bisector. $M$ is the midpoint of line segment $PQ$.

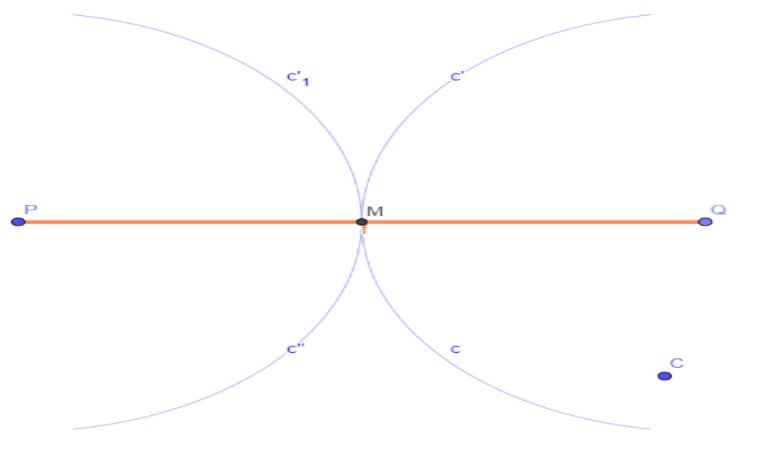
Figure 2 Option A: radii = PM = QM (Incorrect option)

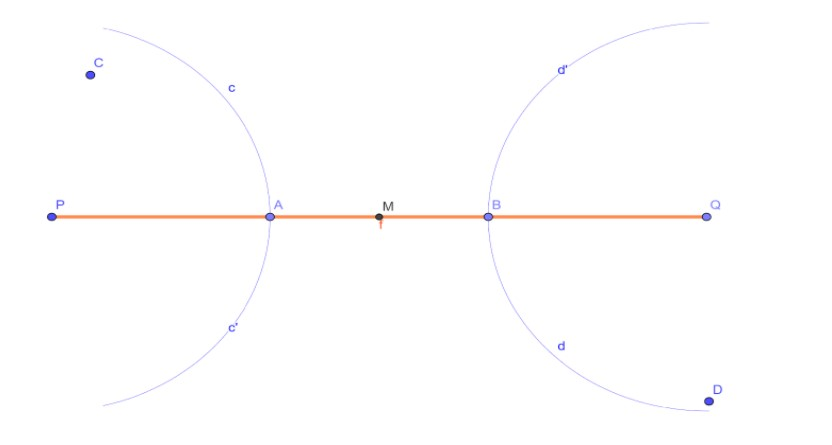
Figure 3 Option B: radii = PA = QB (Incorrect option)

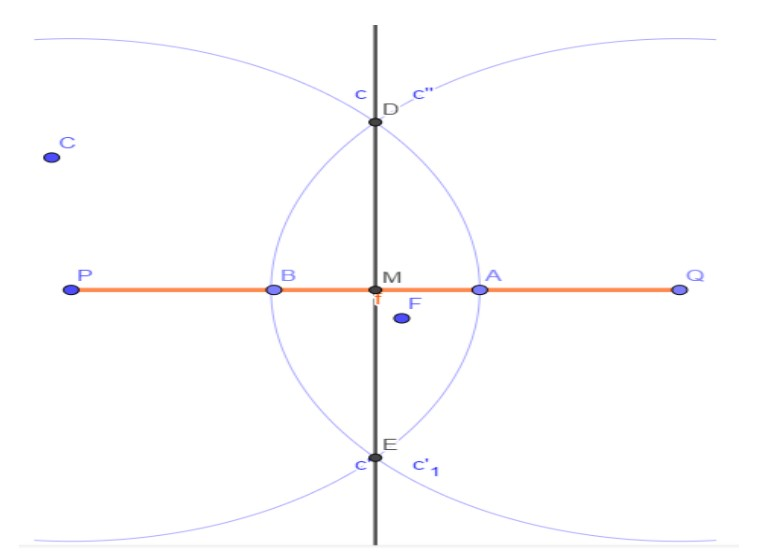
Figure 4 Option C: radii = PA = QB (CORRECT OPTION)

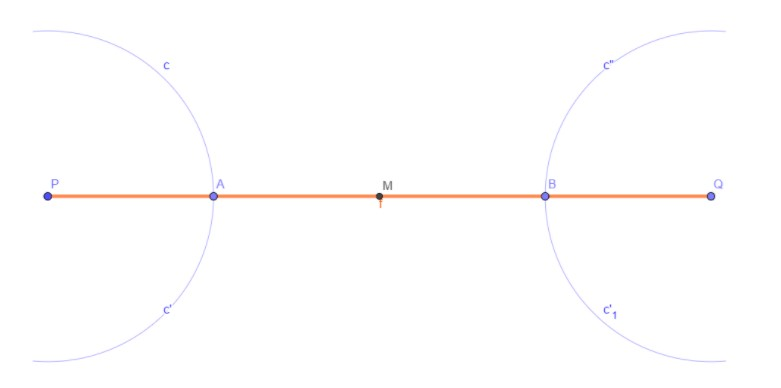
Figure 5 Option D: radii = PA = QB (Incorrect option)