
For series LCR AC circuits shown in figure, the readings of and are the same
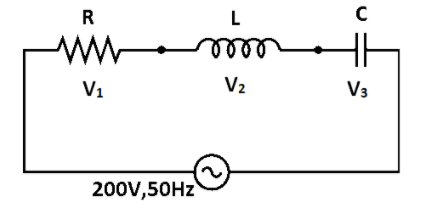
A) The reading
B) The reading of
C) The circuit is in resonant mode
D) The inductive and capacitive reactance are equal.

Answer
497.7k+ views
Hint
For a series LCR circuit, the equation of voltage is given by
Complete step-by-step solution
The resistor, capacitor and the inductor are connected in series. For a series LRC circuit from the phasor diagram we know that,
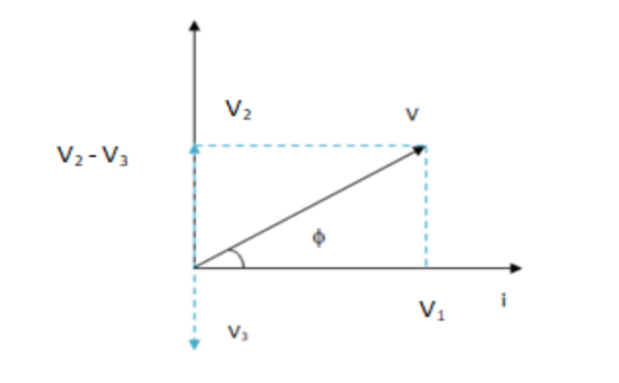
Where,
Given in the question that,
Substitute the voltage readings of capacitor and inductor in the equation of voltage.
Hence, the value of voltage across the resistor is
The correct option above is (A)
Note
For a series LCR circuit, Equation of current:
Impedance of the circuit is given by:
Phase difference is given by:
At resonance, the circuit behaves as a resistive circuit and the whole applied voltage appears across the resistance. The average power and the apparent power are equal at resonance. If the net reactance is inductive, the circuit behaves as an LR circuit. Similarly, when net reactance is capacitive then the circuit behaves as a CR circuit.
For a series LCR circuit, the equation of voltage is given by
Complete step-by-step solution
The resistor, capacitor and the inductor are connected in series. For a series LRC circuit from the phasor diagram we know that,

Where,
Given in the question that,
Substitute the voltage readings of capacitor and inductor in the equation of voltage.
Hence, the value of voltage across the resistor is
The correct option above is (A)
Note
For a series LCR circuit, Equation of current:
Impedance of the circuit is given by:
Phase difference is given by:
At resonance, the circuit behaves as a resistive circuit and the whole applied voltage appears across the resistance. The average power and the apparent power are equal at resonance. If the net reactance is inductive, the circuit behaves as an LR circuit. Similarly, when net reactance is capacitive then the circuit behaves as a CR circuit.
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




