
For the angle of minimum deviation of a prism to be equal to its refracting angle, the prism must be made of a material whose refractive index:
Answer
500.7k+ views
Hint: Firstly we need to draw a diagram to understand the situation clearly. We will use the equation to find the refractive index of a prism and substitute the given situation of angle of minimum deviation in the expression and hence obtain an equation for the refractive index. Then we will apply the limit from
Formula used:
Complete step by step answer:
We will draw the diagram using the parameters, angle of prism as (
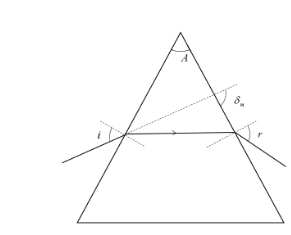
It is given that angle of minimum deviation to be equal to the refracting angle.
Now, we will substitute this in the equation to find the refractive index of prism and it will become,
Now, we will use the trigonometric relation
So, we have the expression for a refractive index.
Now we will apply the limit for angle of prism from
And if
So, we can conclude that the prism could have a refractive index which lies between
So, the correct answer is “Option B”.
Note:
The soul of this question is situated at the part where we are applying the limit for
There we are taking the angles
Formula used:
Complete step by step answer:
We will draw the diagram using the parameters, angle of prism as (

It is given that angle of minimum deviation to be equal to the refracting angle.
Now, we will substitute this in the equation to find the refractive index of prism and it will become,
Now, we will use the trigonometric relation
So, we have the expression for a refractive index.
Now we will apply the limit for angle of prism from
And if
So, we can conclude that the prism could have a refractive index which lies between
So, the correct answer is “Option B”.
Note:
The soul of this question is situated at the part where we are applying the limit for
There we are taking the angles
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




