Question

For the isolated charged conductor shown in the figure, the potentials at points A, B, C and D are ${V_A},{V_B},{V_C}\& {V_D}$ respectively. Then

A. ${V_A} = {V_B} > {V_C} > {V_D}$
B. ${V_D} > {V_C} > {V_B} = {V_A}$
C. ${V_D} > {V_C} > {V_B} > {V_A}$
D. ${V_D} = {V_C} = {V_B} = {V_A}$

Answer 1

Hint: We are given an isolated conductor whose surface is charged. The conductor is non-uniform and thus the charge densities will be different at different areas of the surface. Isolated conductor means that in the whole space, you just consider the conductor alone and nothing else. Check the electric field inside a conductor, what will be the electric field inside a conductor and then use the relation between electric field and electric potential to find the potential at different points inside the conductor.

Complete answer:
First, let us find the electric field inside the conductor.Consider a conductor. As it is a conductor, it will have charges inside it, positive as well as negative. Apply an external field ${\overrightarrow E _{ext}}$. This external electric field will apply force on the charges, positive charges will go in the direction of force and negative charges will go in the opposite direction. These opposite charges will form a new internal electric field such that it cancels the effect of the external electric field. The charges appear on the surface of the conductor and the electric field inside the conductor will be zero.

The relation between the electric field and the electric potential is given as $E = - \dfrac{{dV}}{{dx}}$ where $V$ is electric potential. Consider this equation for the above discussed case. The electric field inside the conductor is zero and hence, we have $E = - \dfrac{{dV}}{{dx}} = 0$ i.e, $V$ is constant. So, the electric potential inside the conductor does not change and is the same everywhere.

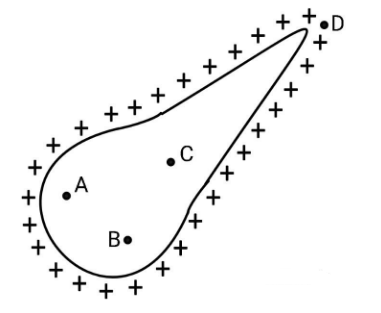
Consider the potential of the surface of the conductor to be ${V_0}$, then the potential at every point inside the conductor will be ${V_0}$ because as you go from surface to any point inside the conductor, the potential will not change and has to be the same as that at the surface. As the point D is on the surface, the potential of point D be ${V_0}$, we will have, ${V_0} = {V_D}$ and as the potential does not change, we will have, ${V_0} = {V_A} = {V_B} = {V_C}$.From the above two derived equations, we have ${V_A} = {V_B} = {V_C} = {V_D}$.

Hence, option D is the correct answer.

Note: Always remember that the electric field inside a conductor is always zero which forces the potential at everywhere point inside the conductor to be the same. Also keep in mind the relation between the electric field and the potential. Also remember the properties we used to make conclusions about the electric field inside a conductor (about the charge distribution).