
For what value of
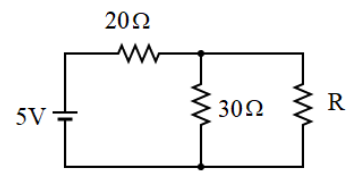

Answer
408.3k+ views
Hint:The concept of power and its formula is applied to determine its value. Kirchhoff's law given by the junction rule for current and the loop rule for voltage is applied in order to determine equations relating the voltage current and resistor values. To determine the maximum power the differentiation is performed.
Complete step by step answer:
The above problem revolves around the concept of power dissipated in a circuit. Let us first know the concept and the definition of power.Power is defined as the rate at which the work is done by a source of emf or voltage supply in maintaining an electric current throughout the circuit. The power is a measure of the heat that is dissipated due to the production of current when there is a voltage supply connected across its circuit elements.
However, in this question we are asked to consider a criteria wherein the power dissipated across
We now apply the equation for ohm’s law which gives the relationship between current and voltage values in a circuit:
This value for
In order to construct equations relating the voltage, current and resistance values given in the circuit we need to apply Kirchhoff's law. This is done in order to find the current that passes through the resistor
The Kirchhoff first law that governs the current in a circuit states that in any electric circuit the algebraic sum of the currents entering a junction is equivalent to the sum of currents leaving that junction. This means that that current is split up at a junction which can be added up to give the total current that had entered the junction. This can be illustrated in the diagram below:
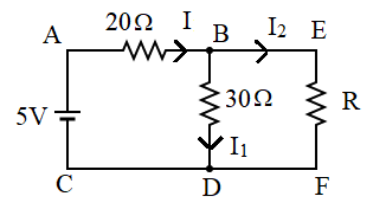
Since we need to find the power with respect to resistor
Our aim is to find out this value of
In order to construct the required equations relating all the quantities we need to apply Kirchhoff's second law or the loop rule which is known as Kirchhoff’s voltage law. The Kirchhoff’s loop rule states that the algebraic sum of the voltages in any closed circuit or loop of a circuit is equal to the sum of the products of currents and resistances in it. This was determined from the ohm’s law relation.
It follows the principle that the sum of the voltage drops across the resistors present in the loop in terms of its currents and resistances given by ohm’s law will be equivalent to the source voltage provided to the circuit. Thus, as per Kirchhoff’s voltage law we first consider the loop through
Next we apply the Kirchhoff’s voltage law to loop
By rearranging the terms to make
This value of
Taking out the common term
By taking the LCM we get:
This above value is substituted into equation (
By further simplifying this equation we get:
We now bring the similar terms together to get:
By taking out the common terms we get:
By taking out the common term
We now get the equation for
Now that we have found out the required current value through resistor
On further simplification:
In order to find the maximum value for power it must be differentiated and equated to zero so as to maximize the value of power that is dissipated. This is because the peak or the maxima of power value is required and hence the slope or the tangent drawn to this peak value in the graph for power that is dissipated in cycles will be parallel to the x-axis, thus making its derivative or slope value equal to zero.Hence, in order to obtain the maximum power we need to differentiate it and equate it to zero and hence we get:
We differentiate the power with respect to
We perform the differentiation by applying the quotient rule and the chain rule for differentiation to get:
Taking out the common term
The common term from the numerator and denominator gets cancelled out to get:
We now perform cross multiplication to get:
By cancelling out the common term
We take the LCM to get:
On further simplification we obtain:
Hence,
Note:A common error that can be observed in this problem is that the equivalence resistance is often calculated and substituted in the power equation which is incorrect. To maximize the power differentiation is required to be carried out. The mathematics and the concept of differentiating must be known in order to solve these types of problems since chain rule and quotient rule must be applied to solve for the value of
Complete step by step answer:
The above problem revolves around the concept of power dissipated in a circuit. Let us first know the concept and the definition of power.Power is defined as the rate at which the work is done by a source of emf or voltage supply in maintaining an electric current throughout the circuit. The power is a measure of the heat that is dissipated due to the production of current when there is a voltage supply connected across its circuit elements.
However, in this question we are asked to consider a criteria wherein the power dissipated across
We now apply the equation for ohm’s law which gives the relationship between current and voltage values in a circuit:
This value for
In order to construct equations relating the voltage, current and resistance values given in the circuit we need to apply Kirchhoff's law. This is done in order to find the current that passes through the resistor
The Kirchhoff first law that governs the current in a circuit states that in any electric circuit the algebraic sum of the currents entering a junction is equivalent to the sum of currents leaving that junction. This means that that current is split up at a junction which can be added up to give the total current that had entered the junction. This can be illustrated in the diagram below:

Since we need to find the power with respect to resistor
Our aim is to find out this value of
In order to construct the required equations relating all the quantities we need to apply Kirchhoff's second law or the loop rule which is known as Kirchhoff’s voltage law. The Kirchhoff’s loop rule states that the algebraic sum of the voltages in any closed circuit or loop of a circuit is equal to the sum of the products of currents and resistances in it. This was determined from the ohm’s law relation.
It follows the principle that the sum of the voltage drops across the resistors present in the loop in terms of its currents and resistances given by ohm’s law will be equivalent to the source voltage provided to the circuit. Thus, as per Kirchhoff’s voltage law we first consider the loop through
Next we apply the Kirchhoff’s voltage law to loop
By rearranging the terms to make
This value of
Taking out the common term
By taking the LCM we get:
This above value is substituted into equation (
By further simplifying this equation we get:
We now bring the similar terms together to get:
By taking out the common terms we get:
By taking out the common term
We now get the equation for
Now that we have found out the required current value through resistor
On further simplification:
In order to find the maximum value for power it must be differentiated and equated to zero so as to maximize the value of power that is dissipated. This is because the peak or the maxima of power value is required and hence the slope or the tangent drawn to this peak value in the graph for power that is dissipated in cycles will be parallel to the x-axis, thus making its derivative or slope value equal to zero.Hence, in order to obtain the maximum power we need to differentiate it and equate it to zero and hence we get:
We differentiate the power with respect to
We perform the differentiation by applying the quotient rule and the chain rule for differentiation to get:
Taking out the common term
The common term from the numerator and denominator gets cancelled out to get:
We now perform cross multiplication to get:
By cancelling out the common term
We take the LCM to get:
On further simplification we obtain:
Hence,
Note:A common error that can be observed in this problem is that the equivalence resistance is often calculated and substituted in the power equation which is incorrect. To maximize the power differentiation is required to be carried out. The mathematics and the concept of differentiating must be known in order to solve these types of problems since chain rule and quotient rule must be applied to solve for the value of
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write a short note on Franklands reaction class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE




