Question

What is the formula for the radius of a semicircle?

Answer 1

Hint: We can write the formula for radius in terms of diameter, circumference or perimeter and area. We know that radius is half of diameter which gives the formula for radius in terms of diameter. The circumference of the semicircle is given by $C=r\left( \pi +2 \right)$ . If we rearrange this formula, we will get the radius in terms of circumference. We know that the area of a semicircle will be half of the area of a circle. From this, we can find r.

Complete step by step solution:
We have to write the formula for radius of a semicircle. Let us see what a semicircle is. When a circle is divided into two equal halves along its diameter, we will get a semicircle. This is illustrated below.

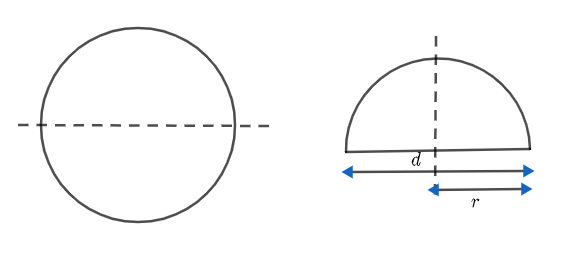
For a circle and semicircle, diameter and hence the radius remains the same.
The formula for radius of semicircle can be written in terms of diameter, circumference or perimeter and area.
Let us write the formula for radius in terms of diameter. We know that radius is half of diameter.
$\Rightarrow r=\dfrac{d}{2}$
Where r is the radius and d is the diameter.
Now, we can write the radius in terms of circumference.
We can write the circumference of a semicircle as $\pi r+2r$ or $r\left( \pi +2 \right)$ by taking r outside since it is the common factor. Let us denote C as the circumference.
$\Rightarrow C=r\left( \pi +2 \right)$
Let us find the radius by taking $\left( \pi +2 \right)$ to the LHS.
\[\Rightarrow r=\dfrac{C}{\left( \pi +2 \right)}\]
Now, let us write the formula for radius in terms of area of a semicircle. Area of a semicircle will be half of area of a circle. We know that area of a circle is $\pi {{r}^{2}}$ . Hence, area, A, of a semicircle is
 $A=\dfrac{\pi {{r}^{2}}}{2}$
Let us take 2 from the RHS to the LHS.
$\Rightarrow 2A=\pi {{r}^{2}}$
The above equation can be written as
$\Rightarrow \dfrac{2A}{\pi }={{r}^{2}}$
Let us take the square root.
$\Rightarrow r=\sqrt{\dfrac{2A}{\pi }}$
Hence, the formulas for radius of semicircle are $r=\dfrac{d}{2}=\dfrac{C}{\left( \pi +2 \right)}=\sqrt{\dfrac{2A}{\pi }}$ .

Note: Students may think that the circumference of a semicircle will be half of that of a circle. This is not true. The area of the semicircle is half that of a circle. Students must note that the diameter and radius of a circle will be the same as that of a semicircle. This doesn’t mean that the formulas for radius of circle and semicircle will be the same.