Question

What is the formula for the surface area of a box?

Answer 1

Hint: Here we have to find the formula for the surface area of a box. Firstly we will form the diagram of the box then we will level all the dimensions of it. As we know a box is either in the shape of a rectangle or a square so we will form a common formula to find the surface area by adding the area of each surface of the box and get our desired answer.

Complete step by step solution:
We have to find the formula for the surface area of a box:
Firstly we will form the diagram a box as follows:

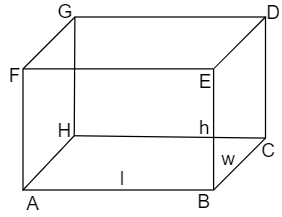
Here we have taken
Height $h=BE$
Length $l=AB$
Width $w=BC$
Now as we can see that the box has six faces all are in rectangle shape.
The top and bottom face have sides as $l$ and $w$…$\left( 1 \right)$
The left and right faces have sides as $h$ and $w$…$\left( 2 \right)$
The front and back face have sides as $l$ and $h$…$\left( 3 \right)$
Next we know the rectangle area is calculated as follows:
Area $=x\times y$
Where, $x,y$ are the two sides
For statement (1) we have area of two faces as:
Area $=2\left( l\times w \right)$…$\left( 4 \right)$
For statement (2) we have area of two faces as:
Area $=2\left( h\times w \right)$…$\left( 5 \right)$
For statement (3) we have area of two faces as:
Area $=2\left( l\times h \right)$….$\left( 6 \right)$
So we will get the surface area of box by adding equation (4), (5) and (6) as follows:
Surface Area of a box $=2\left( l\times w \right)+2\left( h\times w \right)+2\left( l\times h \right)$
Surface Area of a box $=2lw+2hw+2lh$
Hence formula for surface area of a box is $2lw+2hw+2lh$ .

Note:
Box is in the shape of a cuboid or a cube. That is the reason we have taken six sides of it and calculated the area of each side separately. Cuboid is a three-dimensional figure which is made up of six rectangular planes. We can see the common example of cuboid in a brick, pencil box etc. The opposite sides of a cuboid have the same dimension and are always parallel to each other.