Question

Four charges $ {\text{1 mc, 2 mc, 3 mc, }}...{\text{6 mc}} $ are placed on a corner of a square of side $1$ m. The square lies in the $ XY $ plane with its centre at origin?
(A) The electric potential at origin.
(B) The electric potential is zero everywhere along the X axis.
(C) The electric potential is not zero along the Z-axis.
(D) The electric potential is zero along the Z-axis for any orientation of the square in $ XY $ plane.

Answer 1

Hint
In this question, first draw the diagram to represent the given square and the charges at its corner and then calculate the electric potential at the center of the square due to charge at the corner of the square.

Complete step by step answer
In this question, the concept of the electric potential will be used, that is it depends on the quantity of charge and the distance between the point and the charge. We must calculate the potential due to the given charges. So, let us assume that the square is PQRS and charges are placed at the respective corners as shown in figure below.

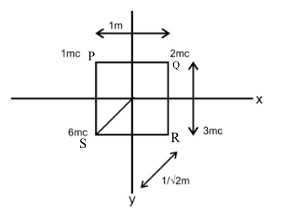
We have to find the effective potential due to the charges present at the corners of the square. We know that the potential at distance $ r $ due a charge $ Q $ kept at corners of the square is given as stated below.
 $ V = \dfrac{{KQ}}{r} $
Here, $ K $ is constant.
As we know that the potential due to charges is given as algebraic sum as the potential is scalar quantity as
 $ V = \dfrac{{K{Q_p}}}{{{r_p}}} + \dfrac{{K{Q_Q}}}{{{r_Q}}} + \dfrac{{K{Q_R}}}{{{r_R}}} + \dfrac{{K{Q_S}}}{{{r_S}}} $
Here, the charges at corner $ P,Q,R $ , and $ S $ are stated as, $ {Q_P},{Q_Q},{Q_R} $ , and $ {Q_S} $ . The distance of the charges and the centre of the square are $ {r_p},{r_Q},{r_R} $ , and $ {r_S} $ . The value of $ K $ is $ 9 \times {10^9} $ .

Now we substitute the given values in the above expression as,
 $ \Rightarrow V = 9 \times {10^9}\left[ {\left( {\dfrac{{1 \times {{10}^{ - 6}}}}{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}}} \right) + \left( {\dfrac{{2 \times {{10}^{ - 6}}}}{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}}} \right) + \left( {\dfrac{{3 \times {{10}^{ - 6}}}}{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}}} \right) + \left( {\dfrac{{6 \times {{10}^{ - 6}}}}{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}}} \right)} \right] $
Now, we solve the above expression to obtain,
 $ \therefore V = 152.73 \times {10^3}\;{\text{V}} $
Since, all the points are equidistant, and the magnitude of the charge is positive so the potential will be non-zero.
After solving the above two equations we get a non-zero potential at origin which is equidistant from the charges and if you look into the image the axis passing through this is $ z - {\text{axis}} $ . So, the potential is nonzero along $ z - {\text{axis}} $ as well.
Therefore, the correct option is (C).

Note
The electric potential at the origin will be zero if the charges at the corner of the diagonals of the square are of same magnitude but opposite sign of charges. The electric potential is a scalar quantity and the electric field is a vector quantity.