Question

From a $10\times 10\times 10$ cube which is formed by combinations of $1\times 1\times 1$ cubes a layer of the smaller cubes is removed. What will be the number of $1\times 1\times 1$ cubes present in this new cube? \[\]
A. 900\[\]

B. 488\[\]

C. 512 \[\]

D. 729\[\]

Answer 1

Hint: We recall the definition of cube and volume cube $V$ which is given with length of the side $a$ as $V={{a}^{3}}$. We see that when we remove a layer of $1\times 1\times 1$ cubes, $10\times 10\times 10$ cube will become $9\times 9\times 9$ cube. We find the number of $1\times 1\times 1$ to make $9\times 9\times 9$ by dividing the volume of $9\times 9\times 9$ by $1\times 1\times 1$ cube. \[\]

Complete step-by-step answer:
We know that a cuboid is a three dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted $l$ , $b$ and $h$. \[\]
A cube is cuboid with all sides of equal length. We denote the length of the side as $a$, then we have
\[l=b=h=a\]
The amount of space contained by a three dimensional object is measured by the quantity called volume. The amount of space that is occupied by a cuboid is the product of length, breadth and height. Mathematically, the volume of a cuboid is $l\times b\times h$. So we calculate the volume of a cube with denoting as $V$.
\[V=l\times b\times h=a\times a\times a={{a}^{3}}\]
We are given the question that $10\times 10\times 10$ cube which is formed by combinations of $1\times 1\times 1$cubes. So the length, breadth and height of the small cube is $a=1$ units. Let its volume be${{V}_{1}}$. So we have volume of small cube in cubic units as,
\[{{V}_{1}}={{a}^{3}}=1\times 1\times 1=1\]
A layer of $1\times 1\times 1$ cube is removed and we show the layer in the figure below.
 

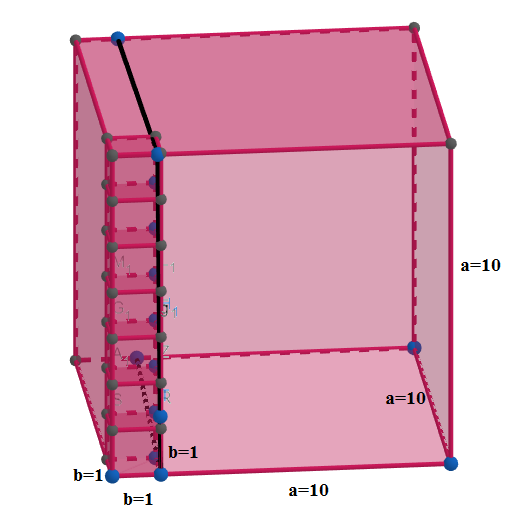
When a layer of $1\times 1\times 1$ cube is removed then the length , breadth and side of the new large cube decreases by 1 unit. So the new cube is of length, breadth and height $10-1=9$ unit. So its volume will be say ${{V}_{9}}$ in cubic units will be
\[{{V}_{9}}=9\times 9\times 9=729\]
So the number of small cubes to make new large cube is,
\[\dfrac{{{V}_{9}}}{{{V}_{1}}}=\dfrac{729}{1}=729\]

So, the correct answer is “Option D”.

Note: We note that the question states ‘a layer of cube’ and we have shown in the figure here a layer at one of the edges of the cube which can be anywhere in the cube. If it would have said ‘outer layer’ to be removed then we would have the new cube of size $8\times 8\times 8$ since we would have to remove layers at all edges of the cube. The number of cubes we removed is ${{V}_{10}}-{{V}_{9}}=1000-729=271$ .