Question

From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be $\alpha $ and $\beta $. Show that the height in miles of aeroplane above the road is given by:
$\dfrac{\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }$

Answer 1

Hint: Use the fact that the distance between two consecutive mile stones is one mile. The angles of depression of two consecutive milestones are given to us. Use the tan ratio for both the angles. That is, the ratio of height and base, where the height is the same for both.

Complete step-by-step answer:
Let us first draw the figure according to the question.

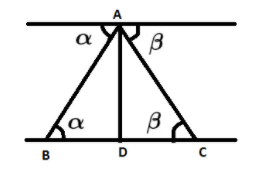
In the above picture A is the aeroplane, B and C are the consecutive mile stones.
We know that the distance between any two consecutive milestones is 1 mile. Therefore,
BC = 1 mile.
AD is the perpendicular from the point A on the line BC, which meets BC at the point D. Therefore the height of the aeroplane is AD.
We can write BC as the sum of BD and DC. Therefore,
$BD+DC=1.....(1)$
The angle of depression of two consecutive milestones are $\alpha $ and $\beta $.
We can see that the angles B and C are alternate interior angles to angles $\alpha $ and $\beta $ respectively. Hence, they will be equal. So, we can write that:
$\angle B=\alpha ,\angle C=\beta $
We also know that the tangent function is the ratio of the perpendicular and base of the triangles ADB and ADC, so here it will be the ratio of perpendicular AD, and the bases BC and CD respectively. Using this condition we will write that-
$\tan \theta = \dfrac{{Perpendicular}}{{Base}} = \dfrac{P}{B}$
$\tan \alpha =\dfrac{AD}{BD}$
$\Rightarrow BD=\dfrac{AD}{\tan \alpha }.......(2)$
And,
$\tan \beta =\dfrac{AD}{DC}$
$\Rightarrow DC=\dfrac{AD}{\tan \beta }......(3)$
Now we will put the values of (2) and (3) in equation (1). Therefore,
$\dfrac{AD}{\tan \alpha }+\dfrac{AD}{\tan \beta }=1$
From the above equation we need to find out the value of AD. Therefore,
$\Rightarrow \dfrac{AD\left( \tan \alpha +\tan \beta \right)}{\tan \alpha \tan \beta }=1$
By cross multiplying,
$\Rightarrow AD\left( \tan \alpha +\tan \beta \right)=\tan \alpha \tan \beta $
By dividing both sides of the equation by $\left( \tan \alpha +\tan \beta \right)$,
$\Rightarrow AD=\dfrac{\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }$
AD is the height of the aeroplane.
Therefore, the height in miles of the aeroplane above the road is:
$\dfrac{\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }$

Note: In this problem the distance between two consecutive mile stones plays a very important role. If we miss that point we will not be able to get the required form of height. Also, a common mistake is that the students may get confused between the formulas for the tangent and the cotangent functions, and may take perpendicular as the base, and base as the perpendicular.