
From the top of a church spire 96 m high the angle of depression of two vehicles on the road at the same level as the base of the spire and on the same side of it are
A. 384 m
B. 672 m
C. 288 m
D. None of these
Answer
464.1k+ views
1 likes
Hint: To do this question, we will first tell that the angle of depression is equal to the angle of elevation and then we will assume the distance between the first car and the church bottom to be ‘x’ m and the second car and the church bottom to be ‘y’ m. then we will draw a labeled figure according to this information. Then we will write the values of
Complete step by step solution:
Here, we have been given the height of the church spire as 96 m and angles of depression on two points on the same side of the church.
We know that the angle of depression is equal to the angle of elevation. Hence, the angle of elevation of the first vehicle to the top of the church is
Now, let us assume the distance from the bottom of the church spire and the first car to be ‘x’ m and the distance between the bottom of the church spire and the second car to be ‘y’ m.
Now, if we draw and label a figure from the above-mentioned information and assumptions, it will look something as follows:
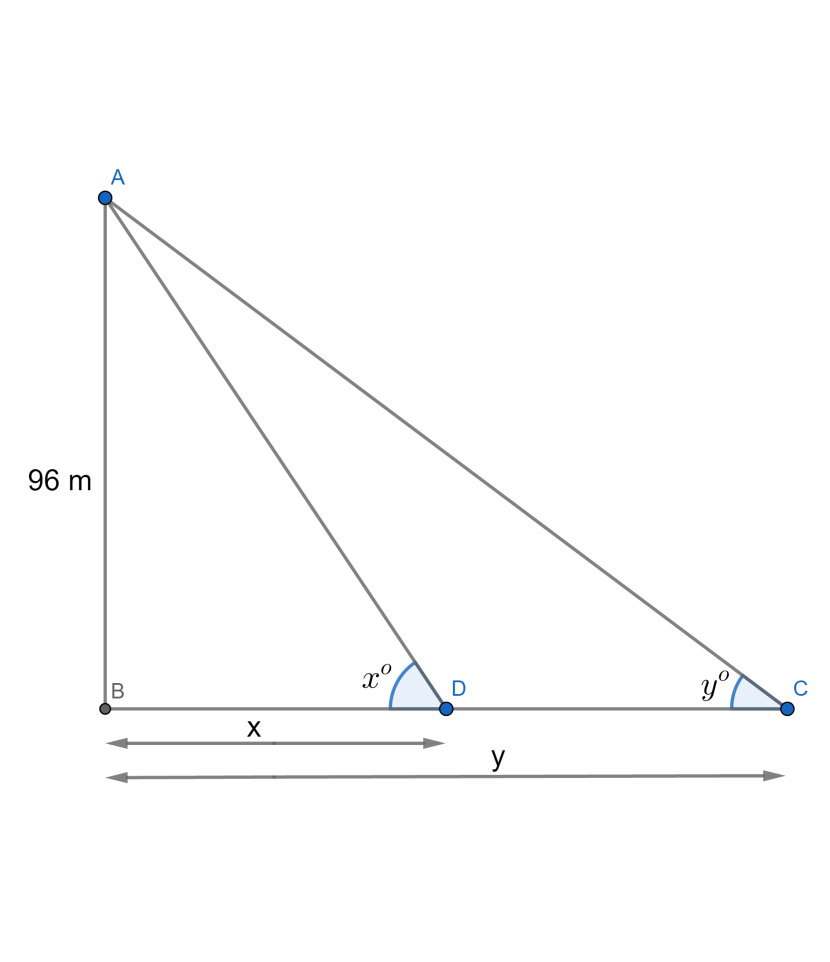
Thus, the distance between the cars will be equal to the difference in the distances between the church bottom and the first car and the church bottom and the second car which will be equal to
Now, we have been given that
We know that in a triangle, the value of tan of an angle is given as:
Now, if we consider the triangle
But we have been given that
Now, solving this, we get the value of x as:
Thus, the distance between the first car and the bottom of the church spire is 384m.
Now, if we consider the triangle
But we have been given that
Now, solving this, we get the value of y as:
Thus, the distance between the second car and the bottom of the church spire is 672m.
Hence, the distance between the cars will be:
Thus, distance between the cars is 288m.
Hence, option (C) is the correct option.
Note:
Here, we have taken tan of both the given angles but we could have taken any of the trigonometric ratios as long as the value of it comes out in the terms of x and y. But we took tan of the angles because the given values are also of the tan of the angles and if we would have taken any other ratio, we would have to convert them into the other. Thus, we took tan.
Complete step by step solution:
Here, we have been given the height of the church spire as 96 m and angles of depression on two points on the same side of the church.
We know that the angle of depression is equal to the angle of elevation. Hence, the angle of elevation of the first vehicle to the top of the church is
Now, let us assume the distance from the bottom of the church spire and the first car to be ‘x’ m and the distance between the bottom of the church spire and the second car to be ‘y’ m.
Now, if we draw and label a figure from the above-mentioned information and assumptions, it will look something as follows:

Thus, the distance between the cars will be equal to the difference in the distances between the church bottom and the first car and the church bottom and the second car which will be equal to
Now, we have been given that
We know that in a triangle, the value of tan of an angle is given as:
Now, if we consider the triangle
But we have been given that
Now, solving this, we get the value of x as:
Thus, the distance between the first car and the bottom of the church spire is 384m.
Now, if we consider the triangle
But we have been given that
Now, solving this, we get the value of y as:
Thus, the distance between the second car and the bottom of the church spire is 672m.
Hence, the distance between the cars will be:
Thus, distance between the cars is 288m.
Hence, option (C) is the correct option.
Note:
Here, we have taken tan of both the given angles but we could have taken any of the trigonometric ratios as long as the value of it comes out in the terms of x and y. But we took tan of the angles because the given values are also of the tan of the angles and if we would have taken any other ratio, we would have to convert them into the other. Thus, we took tan.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




