
From the top of a cliff 200 meters high, the angles of depression of the top and bottom of a tower are
observed to be
between them.
A. Height = 156 m; Distance = 119.7 m
B. Height =
C. Height = 220 m; Distance = 112.76 m
D. None of these.
Answer
472.5k+ views
Hint:If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.
Draw a diagram with the positions of the given structures with respect to the level ground.
Draw some right-angled triangles and identify the given angles in it.
Recall the values of trigonometric ratios for
.g.
Complete step by step solution:
Let's say that AB is the cliff and CD is the tower, as shown in the following diagram:
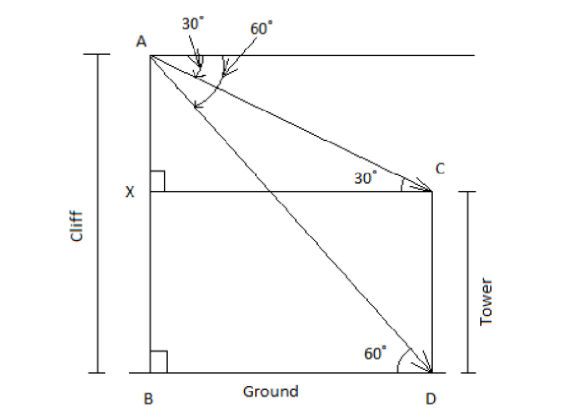
Using the definition of angle of depression and by the properties of parallel lines, we have
Using the definition of
Using
⇒
⇒
Now
we have:
Using
⇒
And
⇒
The correct answer is B. Height =
Note:
In a right-angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
If one trigonometric ratio is known, we can use Pythagoras' Theorem and calculate the values of all other trigonometric ratios.
Draw a diagram with the positions of the given structures with respect to the level ground.
Draw some right-angled triangles and identify the given angles in it.
Recall the values of trigonometric ratios for
.g.
Complete step by step solution:
Let's say that AB is the cliff and CD is the tower, as shown in the following diagram:

Using the definition of angle of depression and by the properties of parallel lines, we have
Using the definition of
Using
⇒
⇒
Now
we have:
Using
⇒
And
⇒
The correct answer is B. Height =
Note:
In a right-angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
If one trigonometric ratio is known, we can use Pythagoras' Theorem and calculate the values of all other trigonometric ratios.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




