Question

From the top of a pillar of height 20 m, the angles of elevation and depression of the top and bottom of another pillar are $ {30^ \circ } $ and $ {45^ \circ } $ respectively. The height of the second pillar (in meters) is:
a) $ \dfrac{{20\left( {\sqrt 3 + 1} \right)}}{{\sqrt 3 }} $
b) $ 10 $
c) $ 10\sqrt 3 $
d) $ \dfrac{{10}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right) $

Answer 1

Hint: The general idea is to draw a tower and make elevation and depression with the given angles to construct another tower. After that the use of trigonometry is going to help to deduce the measurement of the required tower.
Formula used:
From trigonometry in a right angled triangle $ \tan x = \dfrac{p}{b} $ where ‘p’ represents perpendicular and ‘b’ represents base.

Complete step-by-step answer:
Let’s draw the situation first.
We will draw the tower for the reference point and name it AB with length 20 m.
Let’s draw a tower in front of AB and name it CD.
The angle of elevation and depression are $ {30^ \circ } $ and $ {45^ \circ } $ respectively so we will mark it.
Clearly, all the triangles we have here are right angle triangles.
Mark a point ‘E’ lying on CD such that the line BE and AC are parallel.
 We have, AB=CE=20 m

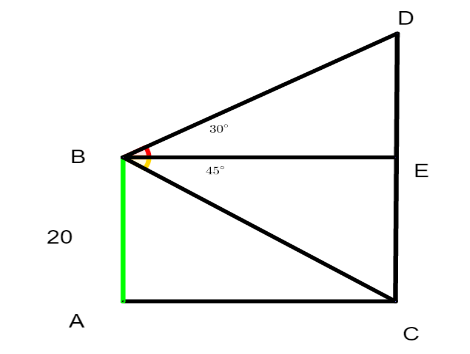
Now in triangle BCE we have, BE as base and CE as perpendicular and $ \angle EBC = {45^ \circ } $ .
So by use of trigonometry we can write,
 $ \tan {45^ \circ } = \dfrac{{CE}}{{BE}} $
 $ \Rightarrow 1 = \dfrac{{20}}{{BE}} \Rightarrow BE = 20 $
Now we have, BE=20 m.
Similarly, in triangle BED we have BE=20 and $ \angle EBD = {30^ \circ } $ using trigonometry we have,
 $ \tan {30^ \circ } = \dfrac{{ED}}{{BE}} $
 $ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{ED}}{{20}} $
 $ \Rightarrow \dfrac{{20}}{{\sqrt 3 }} = ED $
So now the height of tower CD is given by CD=CE+ED
 $ \Rightarrow CD = 20 + \dfrac{{20}}{{\sqrt 3 }} $
 $ \Rightarrow CD = 20\left( {1 + \dfrac{1}{{\sqrt 3 }}} \right) = 20\left( {\dfrac{{\sqrt 3 + 1}}{{\sqrt 3 }}} \right) $
So, the correct answer is “Option A”.

Note: The problems requiring the concept of trigonometry is better solved when it is visualized. So always draw the diagrams with proper labelling and constructions to identify the different angles and sides which will help in solving the question easily.