
Full scale deflection for a galvanometer is
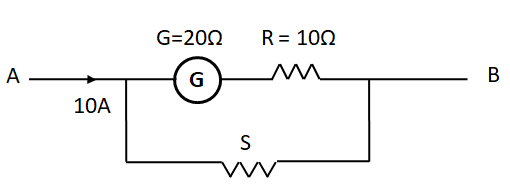
(A)
(B)
(C)
(D)

Answer
483.9k+ views
1 likes
Hint
To solve this question, we have to find out the current through the galvanometer, which is equal to half of the full scale deflection current. Then, using KCL and KVL in the given circuit will give the required value of the shunt resistance.
Complete step by step answer
It is given that the full scale deflection current for the galvanometer is
Now, according to the question, the galvanometer should show half scale deflection, which means that the current which passes through the galvanometer in this case is
Converting in amperes, we get
So, the current distribution in the circuit is as shown in the below diagram.
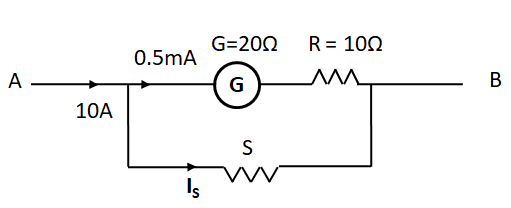
Here
As
Now, as the shunt resistance is connected parallel to the serial combination of the galvanometer and the series resistance, so the potential difference across them will be equal. This gives
According to the question,
On simplifying, we get
Thus, the shunt resistance is equal to
Hence, the correct answer is option (A).
Note
While approximating the current through the shunt resistance as the original current, do not take the current through the galvanometer equal to zero, although applying KCL will give it equal to zero. We have to take care of the fact that the galvanometer is a very much sensitive device. So it shows the deflection even for a negligibly small amount of current which flows through it. Hence, even the negligibly small value can’t be neglected for a galvanometer.
To solve this question, we have to find out the current through the galvanometer, which is equal to half of the full scale deflection current. Then, using KCL and KVL in the given circuit will give the required value of the shunt resistance.
Complete step by step answer
It is given that the full scale deflection current for the galvanometer is
Now, according to the question, the galvanometer should show half scale deflection, which means that the current which passes through the galvanometer in this case is
Converting in amperes, we get
So, the current distribution in the circuit is as shown in the below diagram.

Here
As
Now, as the shunt resistance is connected parallel to the serial combination of the galvanometer and the series resistance, so the potential difference across them will be equal. This gives
According to the question,
On simplifying, we get
Thus, the shunt resistance is equal to
Hence, the correct answer is option (A).
Note
While approximating the current through the shunt resistance as the original current, do not take the current through the galvanometer equal to zero, although applying KCL will give it equal to zero. We have to take care of the fact that the galvanometer is a very much sensitive device. So it shows the deflection even for a negligibly small amount of current which flows through it. Hence, even the negligibly small value can’t be neglected for a galvanometer.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




