Question

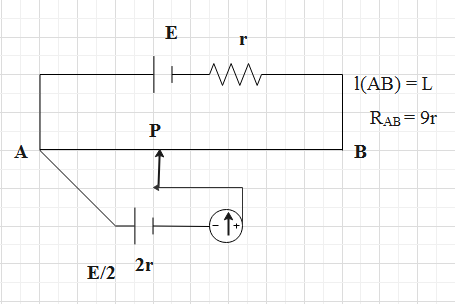
Galvanometer shows no deflection when length AP is

\[A.\,\dfrac{4L}{9}\]
\[B.\,\dfrac{5L}{9}\]
\[C.\,\dfrac{7L}{18}\]
\[D.\,\dfrac{11L}{18}\]

Answer 1

Hint: The galvanometer shows zero deflection when the resistances of on both the sides of the galvanometer are equal to each other. In other words, when no current passes through the galvanometer, it shows zero deflection. Firstly, we will compute the equivalent resistance value. Using this, we will compute the current through AB. Then, we will use the formula of the potential drop across line AP to find the value of the length AP.
Formula used:
\[I=\dfrac{V}{R}\]
\[V=I\times \rho l\]

Complete answer:
The galvanometer will show zero deflection, when, initially the rheostat will have zero resistance value. We will make use of Ohm’s formula.
Let us compute the equivalent resistance of the system. So, we have,
\[{{R}_{eq}}={{R}_{AB}}+r\]
Substitute the value of the resistance between the points A and B.
\[\begin{align}
  & {{R}_{eq}}=9r+r \\
 & \Rightarrow {{R}_{eq}}=10r \\
\end{align}\]
Thus, with the help of this value, we will compute the flow of current through line AB.
\[\begin{align}
  & {{I}_{AB}}=\dfrac{V}{{{R}_{eq}}} \\
 & \Rightarrow {{I}_{AB}}=\dfrac{E}{10r} \\
\end{align}\]
We have used E, in the place of voltage, as in the diagram its mentioned.
The amount of flow of current through the line AB is equal to the amount of flow of current through the line AP. So, the amount of flow of current through the line AP is,
\[{{I}_{AP}}=\dfrac{E}{10r}\]…… (1)
The potential drop across the line AP is given as follows.
\[{{V}_{AP}}={{I}_{AP}}\times \rho l\]
Where \[\rho \]is the resistance per unit length and l is the length of the line AP.
Here, the value of the resistance per unit length is \[\dfrac{9r}{L}\]. The potential drop across the line AP is given to be equal to \[\dfrac{E}{2}\].
Substitute these above values and the value of the equation (1) in the above equation of the potential drop.
\[\dfrac{E}{2}=\dfrac{E}{10r}\times \dfrac{9r}{L}\times {{l}_{AP}}\]
Continue further calculation.
\[\begin{align}
  & \dfrac{1}{2}=\dfrac{1}{10}\times \dfrac{9}{L}\times {{l}_{AP}} \\
 & \Rightarrow {{l}_{AP}}=\dfrac{5L}{9} \\
\end{align}\]

So, the correct answer is “Option B”.

Note:
In this question, we have made use of Ohm’s law equation, the formula of the potential drop. These two equations are the most important. While calculating the current through AB, we have used the complete potential value, whereas, while calculating the current through AP, we have used the half the value of the complete potential value.