Question

What is the general equation of a plane which is parallel to x-axis?
(a) ax+ by + cz + d = 0, a $\ne $ 0, b $\ne $ 0, c $\ne $ 0.
(b) ax+ by + d = 0, a $\ne $ 0, b $\ne $ 0.
(c) by + cz + d = 0, b $\ne $ 0, c $\ne $ 0.
(d) ax + cz + d = 0, b $\ne $ 0, c $\ne $ 0.

Answer 1

Hint: To solve this question we first need to know that what is the equation of the x-axis i.e. it is given by $\dfrac{x}{1}=\dfrac{y}{0}=\dfrac{z}{0}$. And from the equation we can see that the direction cosine of the x-axis are
< 1, 0, 0 > so if we assume the equation of the plane as ax + by + cz + d = 0, then the normal of the plane will be perpendicular to the x-axis as plane is given parallel to x-axis. So we will make the dot product of the direction cosines of the plane and the x-axis to be zero and from there we will get our answer.

Complete step by step answer:
We have to find the general equation of the plane parallel to the x-axis,
For this first we need to know that equation of the x-axis,
Equation of the x-axis is given by = $\dfrac{x}{1}=\dfrac{y}{0}=\dfrac{z}{0}$
Now we can see that direction cosines of the x-axis are < 1, 0, 0 >
Now to find the general equation we will assume the equation of the plane as,
$ax+by+cz+d=0\,\,\,...\left( 1 \right)$
Now we know that if this plane is parallel to x-axis then this plane’s normal will be perpendicular to the x-axis,
So we know that for the two lines if they are perpendicular then the dot product of their direction cosines is zero,
And direction cosine of the normal to the plane is given as,
< a, b, c >
Now we will do the dot product like as following,
$\begin{align}
  &\Rightarrow \left( \begin{matrix}
   a & b & c \\
\end{matrix} \right).\left( \begin{matrix}
   1 & 0 & 0 \\
\end{matrix} \right)=0 \\
 &\Rightarrow a\times 1+b\times 0+c\times 0=0 \\
 &\Rightarrow a=0 \\
\end{align}$
Now putting this value in equation 1 we get,
$\begin{align}
  & \Rightarrow ax+by+cz+d=0 \\
 &\Rightarrow 0\times x+by+cz+d=0 \\
 &\Rightarrow by+cz+d=0 \\
\end{align}$

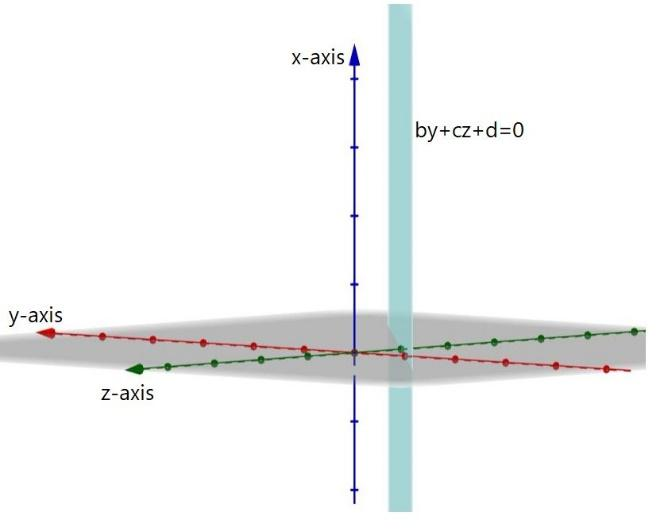
So, the correct answer is “Option C”.

Note: To solve these kinds of problems we should have some prior knowledge of the 3D vectors or geometry so you need to go through the simple topics of the chapter to gather the basic knowledge about these concepts. And also remember the mentioned formula for the equation of the x-axis for future problems.