Question

Give the relation between focal length and radius of curvature.

Answer 1

Hint: The focal length (f) is the distance between the centre of the lens to the principal foci or the point of focus. The radius of the mirror from which the mirror was cut is known as the radius of curvature (R). Here we derive a relation between the focal length and the radius of curvature with the help of a ray diagram.

Complete step by step answer:

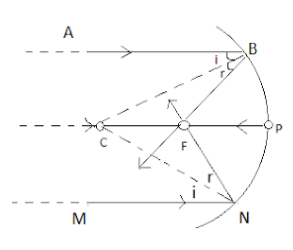
Let us consider that a ray of light AB is parallel to the principal axis and is incident on the spherical mirror.
After reflection, the ray AB passes through the point Focus F on the principal axis CP.
Also, BC is the normal to the spherical mirror at point B.
According to the law of reflection – Angle of incident is always equal to the angle of reflection.
$$\begin{gathered} \therefore \mathrm{\angle }i=\mathrm{\angle }r \\ \Rightarrow \mathrm{\angle }ABC=\mathrm{\angle }CBF......\text{(1)} \end{gathered}$$
Also, we know that lines AB and CP are parallel to each other.
Therefore, by using the property of the parallel lines- we get alternate angles equal.
$\mathrm{\angle }ABC=\mathrm{\angle }BCP.....\text{(2)}$
By using equations $(1)\text{ and (2)}$ we can say that $\mathrm{\Delta }BCF$ is an isosceles triangle.
$\Rightarrow BF=CF....\text{(3)}$
The aperture of the mirror being very small, the point B would be very close to point P.
$\Rightarrow BF=PF....\text{(4)}$
By using equations $(3)\text{ and (4)}$
Since the left hand side of both the equations are equal and same, we can write both its right hand side equal.
$\Rightarrow CF=PF$
Since we have point F on the line PC, we can write PF has the sum of PF and CF.
$PC=PF+CF$
Also, PF and CF both are equal.
$\Rightarrow PC=2PF$
Now, by definition we have PF equal to focal length and PC equal to the radius of the curvature.
We can write above equation as-
$R=2f$
It implies that the radius of curvature is twice the focal length.

Note:
Always remember the basic properties of the parallel lines and its transversal. Refer different angles formed by two parallel lines. Follow the law of the reflection which states that when the ray of light reflects on the surface, the angle of incidence is equal to the angle of reflection. Know the difference between the law of refraction which is also known as Snell’s law which is based on the refractive index.